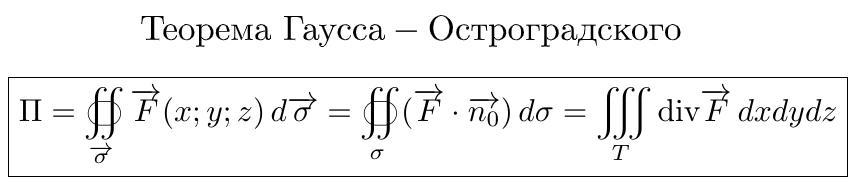Question

Завдання з вищої математики

Answer 1

Ответ:

Поток векторного поля через замкнутую поверхность с внешней нормалью:

$\boldsymbol{\boxed{\displaystyle \Pi =-\frac{1}{2} }}$

Примечание:

Теорема Остроградского - Гаусса:

(нормаль внешняя)

(см. полную формулировку на фото)

$\boldsymbol{\boxed{\displaystyle \Pi = \iiint\limits_{T} \text{div} \overrightarrow{F} \, dx dydz}}$

$T$ - тело, которое ограничивает поверхность

$\overrightarrow{F}(x;y;z) = P(x;y;z)\overrightarrow{i} + Q(x;y;z)\overrightarrow{j} + R(x;y;z)\overrightarrow{k}$ - векторное поле

$\overrightarrow{n_{0}}$ - единичная нормаль

Ротор векторного поля $\overrightarrow{F}(x;y;z) = P(x;y;z)\overrightarrow{i} + Q(x;y;z)\overrightarrow{j} + R(x;y;z)\overrightarrow{k}$:

$\boxed{\text{div} \overrightarrow{F} = \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}}$

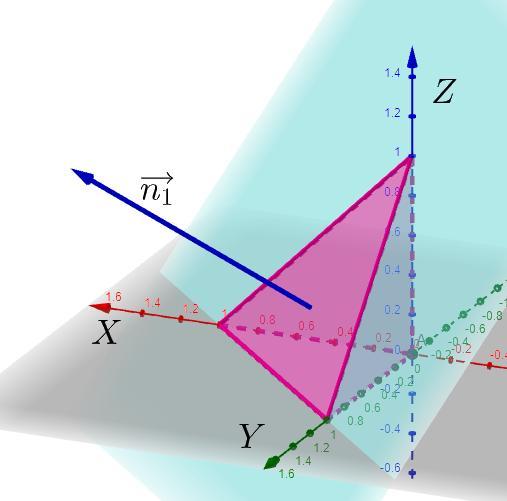
(на иллюстративном рисунке оси координат и вектор $\overrightarrow{n_{1}}$ рисунке являются векторами нормали к соответствующим плоскостям)

Пошаговое объяснение:

Нормаль внешняя

Векторное поле $\overrightarrow{a}$:

$\overrightarrow{a} = (yz - x)\overrightarrow{i} + (x^{2} -1)\overrightarrow{j} + (xy - 2z)\overrightarrow{k}$

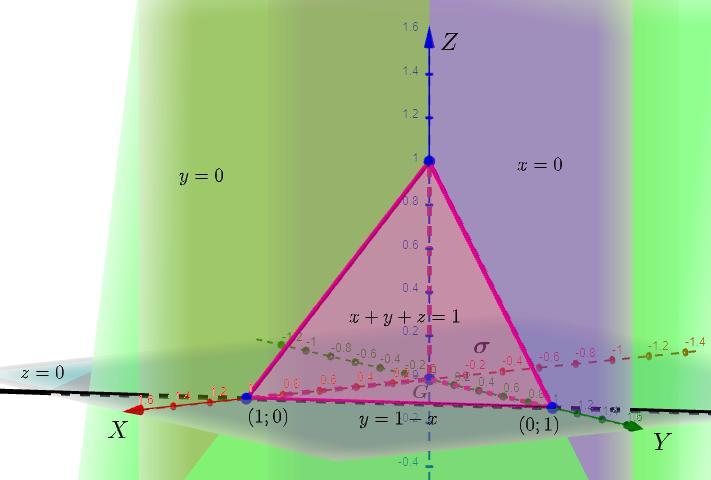
Замкнутая поверхность:

$\sigma:$

$x + y + z = 1 \Longrightarrow z = 1 - x - y$

$x = 0$

$y = 0$

$z = 0$

Ротор векторного поля $\overrightarrow{a}:$

$\dfrac{\partial P}{\partial x} = \dfrac{\partial }{\partial x} \bigg(yz - x \bigg) =-1$

$\dfrac{\partial Q}{\partial y} = \dfrac{\partial }{\partial y} \bigg(x^{2} -1 \bigg) = 0$

$\dfrac{\partial R}{\partial z} = \dfrac{\partial }{\partial z} \bigg(xy - 2z \bigg) = -2$

$\text{div} \overrightarrow{F} = \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z} =-1 + 0 -2 =-3$

Поток векторного $\overrightarrow{a}$ поля сквозь замкнутую поверхность $\sigma$ с внешней нормалью:

$\displaystyle \Pi = \iiint\limits_{\sigma} \text{div} \overrightarrow{F} \, dx dydz =\iiint\limits_{\sigma} -3 \, dx dydz = -3\iiint\limits_{\sigma} \, dx dydz$

Проектировать будем на плоскость $XY$, поэтому сведем тройной интеграл к повторному следующим образом:

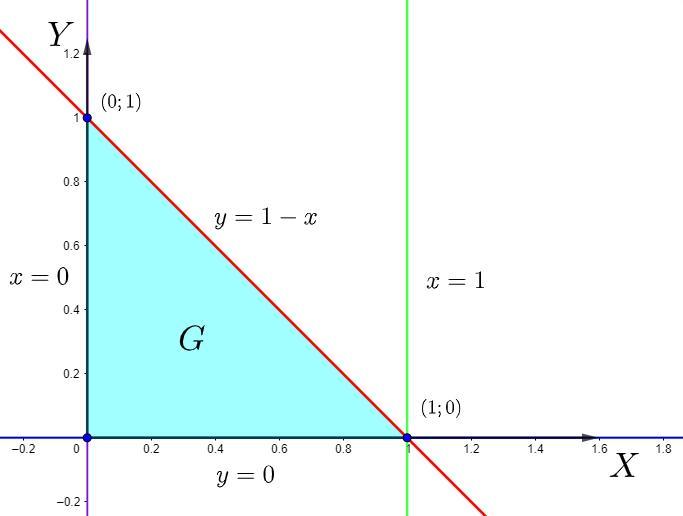
$\displaystyle -3\iiint\limits_{\sigma} dxdydz = -3\Bigg( \iint\limits_{G} dxdy \int\limits^{1 - x - y}_{0} \, dz \Bigg)$, где $G \ -$ проекция на плоскость $XY$; для того, чтобы расставить границы интегрирования, условно говоря, "пронзаем" тело вдоль оси Z с плоскости z = 0, до плоскости z = 1 - x - y.

Распишем приведение двойного интеграла $\displaystyle \iint\limits_{G} dxdy$ к повторному:

Для вычисления двойного интеграла сведем его к повторному интегралу. Будем интегрировать по x, поэтому найдем прямые пересечения плоскости  z = 0 и плоскости z = 1 - x - y:

0 = 1 - x - y

y = 1 - x

Точка пересечения плоскости x = 0 и прямой y = 1 - x:

(0;1)

Точка пересечения плоскости y = 0 и прямой y = 1 - x:

(1;0)

Приведения двойного интеграла к повторному интеграла по области $G$ будет в виде:

$\displaystyle \iint\limits_{G} dxdy = \int\limits^{1}_{0} \, dx \int\limits^{1 - x}_{0} \, dy$

Таким образом тройной интеграл расписывается следующим образом:

$\displaystyle \Pi = -3\iiint\limits_{\sigma} \, dx dydz = -3\Bigg( \iint\limits_{G} dxdy \int\limits^{1 - x - y}_{0} \, dz \Bigg) = -3\Bigg( \int\limits^{1}_{0} \, dx \int\limits^{1 - x}_{0} \, dy \int\limits^{1 - x - y}_{0} \, dz \Bigg) =$

$\displaystyle = -3\Bigg( \int\limits^{1}_{0} \, dx \int\limits^{1 - x}_{0} \bigg( z \bigg |^{1 -x -y}_{0} \bigg) \, dy \Bigg) =-3\Bigg( \int\limits^{1}_{0} \, dx \int\limits^{1 - x}_{0} \bigg( 1 -x -y - 0 \bigg) \, dy \Bigg) =$

$\displaystyle=-3\Bigg( \int\limits^{1}_{0} \, dx \int\limits^{1 - x}_{0} \bigg( 1 -x -y\bigg) \, dy \Bigg) = -3 \int\limits^{1}_{0} \Bigg( \bigg(y(1- x) -\frac{y^{2}}{2} \bigg ) \bigg |_{0}^{1 - x} \Bigg) \, dx =$

$\displaystyle = -3 \int\limits^{1}_{0} \Bigg( \bigg((1 - x)(1- x) -\frac{(1 - x)^{2}}{2} \bigg ) \bigg |_{0}^{1 - x} \Bigg) \, dx = -\frac{3}{2} \int\limits^{1}_{0} {(1 - x)^{2}} \, dx =$

$\displaystyle = \frac{3}{2} \int\limits^{1}_{0} {(1 - x)^{2}} \, d(1 - x) = \dfrac{3}{2} \cdot \frac{1}{3} \cdot (1- x)^{3} \bigg|_{0}^{1} = \frac{1}{2} \bigg((1 - 1)^{1} - (1 -0)^{3} \bigg) =$

$= -1 \cdot \dfrac{1}{2} = -\dfrac{1}{2}$