Question

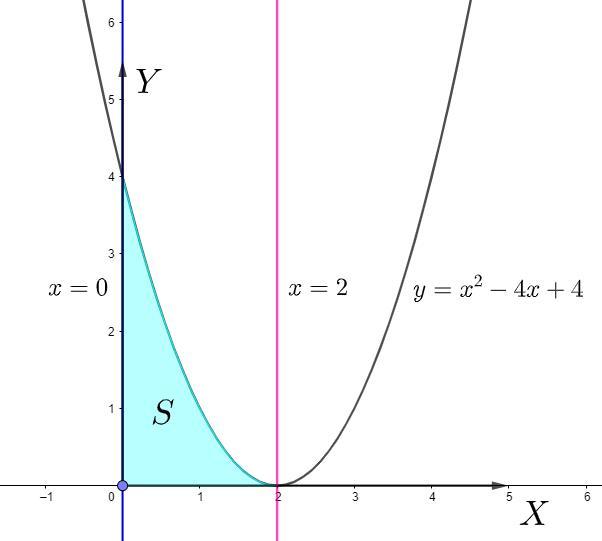
Найдите площадь фигуры, ограниченой указанами линиями

Answer 1

Ответ:

Площадь фигуры равна $\boldsymbol{\dfrac{8}{3}}$ квадратных единиц

Пошаговое объяснение:

Линии ограничивающие фигуру:

$y = x^{2} - 4x + 4$

$y = 0$

$x = 0$

Точки пересечения:

$y(0) = 0^{2} - 4 \cdot 0 + 4 = 4 \Longrightarrow (0;4) \ -$ точка пересечения

$x^{2} - 4x + 4 = 0$

$(x - 2)^{2} = 0 \Longleftrightarrow x - 2 = 0 \Longrightarrow x = 2$

Следовательно точка пересечения $(2;0)$

По определению значение определенного интеграла есть площадь под графиком $f(x)$ ограниченная графиком , прямыми x = a, a = b,

b > a и y = 0, то есть:

$\displaystyle S = \int\limits^a_b {f(x)} \, dx$

$\displaystyle S = \int\limits^2_0 {(x^{2} - 4x + 4)} \, dx = \int\limits^2_0 {(x - 2)^{2}} \, dx= \int\limits^2_0 {(x - 2)^{2}} \, d(x - 2)=$

$= \dfrac{1}{3} \cdot (x - 2)^{3} \bigg|_{0}^{2} = \dfrac{1}{3} \bigg((2 - 2)^{3} - (0 - 2)^{3} \bigg) = \dfrac{2^{3}}{3} = \dfrac{8}{3}$ квадратных единиц.