Предмет: Алгебра,
автор: medded
Для функции y=f(x) найдите первообразную, которая удовлетворяет условие F(1)=3
Приложения:
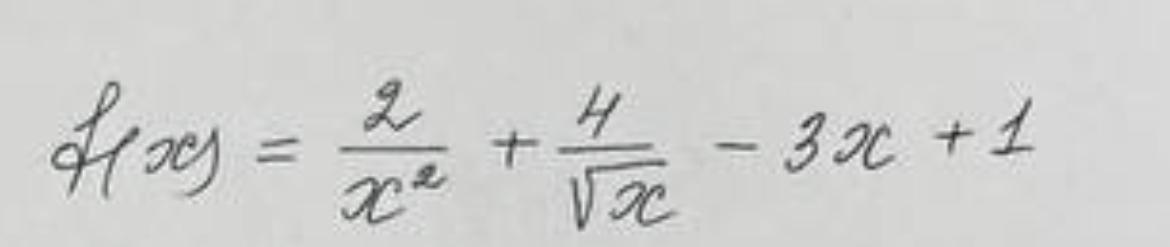
Ответы
Автор ответа:
0
Ответ:
Первообразная для функции f(x) равна
Условие
.
Значит, первообразная, удовлетворяющая указанным условиям, равна
selfcare39:
здравствуйте, помогите пожалуйста с алгеброй задание у меня в профиле отмечу 5 звёзд и сделаю лучший ответ
Похожие вопросы
Предмет: Українська мова,
автор: kucanastasia47
Предмет: Українська мова,
автор: olenaberezuk04012011
Предмет: Українська мова,
автор: foxclub1737
Предмет: Русский язык,
автор: anastasiya2704
Предмет: Алгебра,
автор: ekaterinakanksep5876