Предмет: Алгебра,
автор: nickname11111123
Упростите выражение. 11 класс. Не понимаю что делать, а очень бы хотель.
Приложения:
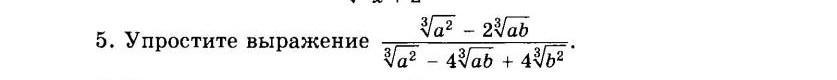
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Формула для решения - квадрат разности:
Автор ответа:
0
Ответ:
Упрощенное выражение:
Объяснение:
Воспользуемся свойством корня нечетной степени из произведения:
.
В числителе вынесем за скобки общий множитель, в знаменателе применим формулу сокращенного умножения:
x² - 2xy + y² = (x - y)²
Получим:
сокращаем дробь и получаем:
Похожие вопросы
Предмет: Українська мова,
автор: foxclub1737
Предмет: Русский язык,
автор: csek64128
Предмет: Қазақ тiлi,
автор: marzhan7718
Предмет: Математика,
автор: Pojkikj
Предмет: История,
автор: ema1252