Предмет: Математика,
автор: kentparlament7771337
Обчислити площу плоскої фігури, обмеженої лініями:
Приложения:
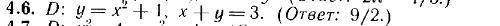
Ответы
Автор ответа:
3
Ответ:
S = 4,5 (eд)²
Пошаговое объяснение:
Обчислити площу плоскої фігури, обмеженої лініями: y = x² + 1 , x + y = 3
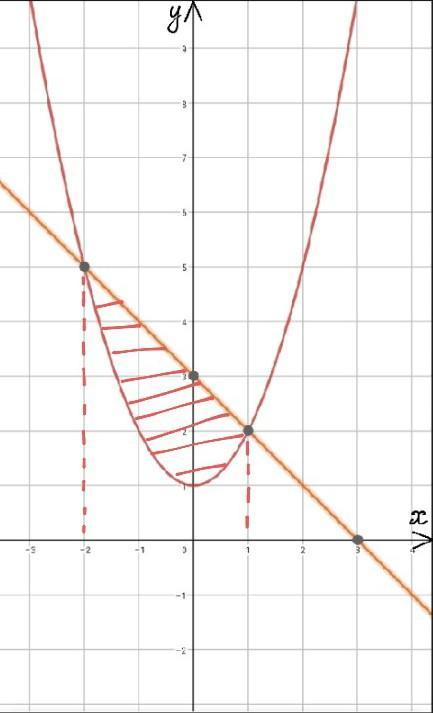
Графиком данной функции является - парабола , которая сдвинута вдоль оси Оу на 1 ед вверх. Вершина параболы в точке ( 0 ; 1 ) .
Выразим у :
Это линейная функция , графиком которой является - прямая . Найдем точки пересечения данных функций :
Пересечение графиков в точках ( -2 ; 5 ) и ( 1 ; 2 ) , пусть 3-я точка будет точкой пересечения линейной функции с осью Ох :
Абсциссы точек пересения графиков это : -2 и 1 , значит , интегрировать будем на этом промежутке. Заметим , на промежутке ( -2 ; 1 ) функция y = -x + 3 больше чем y = x² + 1 , поэтому , при интегрировании из второй функции отнимем первую.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: nikakarmazina2010
Предмет: Геометрия,
автор: Rol4ek
Предмет: Русский язык,
автор: kaumovaalina1153
Предмет: История,
автор: sbgfyhnuyyukf
Предмет: Биология,
автор: snikbox