Question

Решить задачу (пожалуйста, поподробней):

Поезд движется по закруглению радиусом R = 100 м, причем

зависимость его координаты от времени дается уравнением x = Ct³ , где

С = 10 м/с³ – постоянная величина. Найти полное ускорение поезда α в тот

момент, когда его скорость υ=54 км/ч.

Ответ должен получится: а = 4,8 м/с²

Answer 1

Ответ:

Полное ускорение поезда равно приблизительно 42,5 м/c²

Примечание:

$\overrightarrow{a_{\tau}} \perp \overrightarrow{a_{n}}$

Объяснение:

Дано:

R = 100 м

$x = Ct^{3}$

$C =$ 10 м/с³

$v =$ 54 км/ч = 15 м/c

Найти:

$a \ - \ ?$

--------------------------------------

Решение:

Механический смысл производной:

$v = x' = (Ct^{3})' = 3Ct^{2}$ - скорость от времени

$a = x'' = (Ct^{3})'' = ((Ct^{3})')' = (3Ct^{2})' = 6Ct$

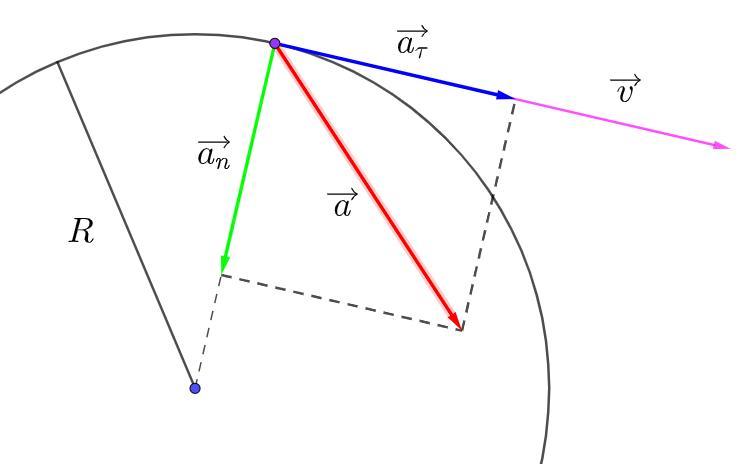
Нормальное ускорение (центростремительное):

$\boxed{a_{n} = \dfrac{v^{2}}{R}}$

Для нахождения тангенциального ускорения составим систему уравнений:

$\displaystyle \left \{ {{a_{\tau} = 6Ct} \atop {v=3Ct^{2} }} \right \ \left \{ {{a_{\tau} = 6Ct} \atop {t = \sqrt{\dfrac{v}{3C} } }} \right \Longrightarrow \boxed{ {a_{\tau} = 6C\sqrt{\dfrac{v}{3C}} }}$

Полное ускорение:

$a = \sqrt{a_{\tau}^{2} + a_{n}^{2}} = \sqrt{ \Bigg(6C\sqrt{\dfrac{v}{3C}} \Bigg)^{2} + \Bigg(\dfrac{v^{2}}{R} \Bigg)^{2} } = \sqrt{\dfrac{36vC^{2}}{3C} + \dfrac{v^{4}}{R^{2}} } =\sqrt{v \Bigg(12C + \dfrac{v^{3}}{R^{2}} \Bigg)}$

$\boldsymbol{\boxed{a = \sqrt{v \Bigg(12C + \dfrac{v^{3}}{R^{2}} \Bigg)}}}$

Расчеты:

$\boldsymbol a =$ √(15 м/c(12 · 10 м/с³ + (3 375 м³/с³ / 10 000 м²) )) $\boldsymbol \approx$ 42,5 м/c²

Ответ: $a \approx$ 42,5 м/c².