Question

СРОЧНО!! ДАЮ 100 БАЛОВ
В прямоугольнике ABCD диагональ вдвое больше его меньшей стороны. Чему равен угол между большей стороной прямоугольника и его диагональю? Если большая сторона прямоугольника равна корень из 5,то чему равна его площадь?

Answer 1

Ответ:

30° угол между большей стороной прямоугольника и его диагональю

$\dfrac{5\sqrt{3} }{3}$ его площадь

Объяснение:

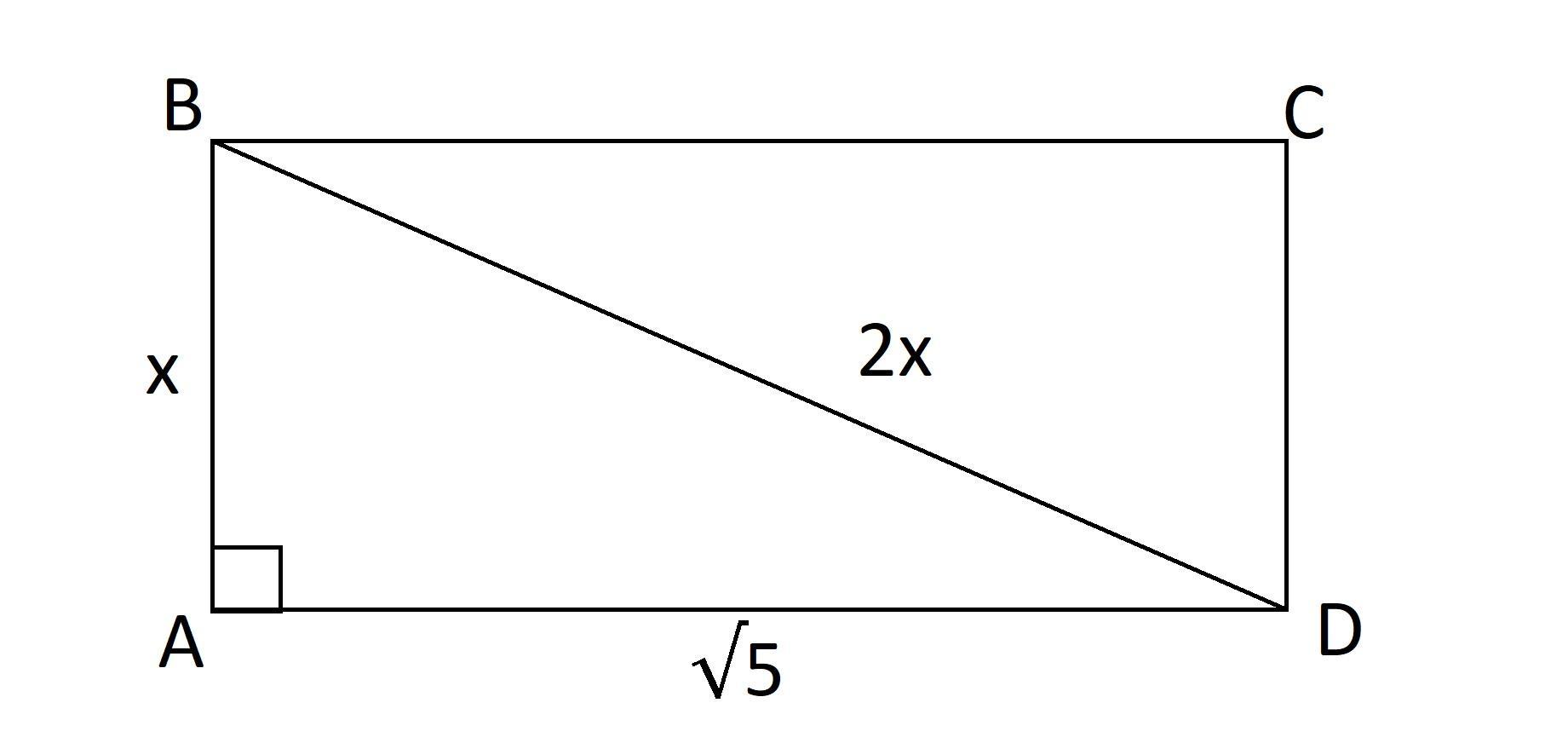
Нарисуем диагональ ВD.

Рассмотрим ΔАВD: ∠ВАD=90° ⇒ ΔАВD прямоугольный

Обозначим АВ как х, а ВD как 2х, тогда по теореме Пифагора:

(2х²)=х²+(√5)²

4х²=х²+5

4х²-х²=5

3х²=5

х²=5/3

х=√(5/3) сторона АВ

$tgADB=\dfrac{AB}{AD} =\dfrac{\sqrt{\dfrac{5}{3} } }{\sqrt{5} } =\dfrac{\dfrac{5\sqrt{3} }{3} }{5} =\dfrac{\sqrt{3} }{3}$

∠АDВ=30° - табличное значение

$S=AB*AD=\sqrt{\dfrac{5}{3} } *\sqrt{5} =\dfrac{5\sqrt{3} }{3}$

Answer 2

Дано:

--------------------------------------------------------

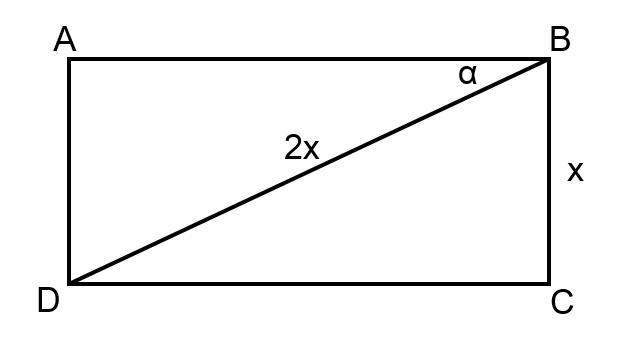
прямоугольник ABCD (приложение)

диагональ BD = 2BC

AB = $\sqrt 5$

--------------------------------------------------------

∠α - ?

Sabcd - ?

Решение:
∠ABD = ∠BDC = ∠α (при AB || CD и секущей BC, т.к. ABCD - прямоугольник по условию)

∠D = 90° (ABCD - прямоугольник по условию)   =>   ΔBCD - прямоугольный

по т. Пифагора:

$CD=\sqrt{(2x)^2-x}=x\sqrt3$

$\angle \alpha=\dfrac{x\sqrt3}{2x}=\dfrac{\sqrt3}2\quad = > \quad \angle\alpha=30^{\circ}$

$x\sqrt3=\sqrt5\\\\x=\dfrac{\sqrt5}{\sqrt3}$

$S_{ABCD}=x\cdot x\sqrt3=\dfrac{\sqrt5}{\sqrt3}\cdot\sqrt5=\dfrac{5}{\sqrt3}=\dfrac{5\sqrt3}3$