Предмет: Алгебра,
автор: 15sdxqwd
Оцените значение выражения
Приложения:
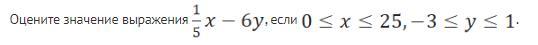
Ответы
Автор ответа:
3
Ответ:
Объяснение:
Оценить значение выражения:
, если
.
- Если умножить все части неравенства на положительное число, знак неравенства не изменится.
- Если умножить все части неравенства на отрицательное число, знак неравенства перевернется.
или
- Если почленно сложить два неравенства одного знака, то получим верное неравенство.
Похожие вопросы
Предмет: Русский язык,
автор: wsafgvbj
Предмет: История,
автор: n394961
Предмет: Русский язык,
автор: hsuiosop
Предмет: Английский язык,
автор: ртнетг
Предмет: Информатика,
автор: amnat2006