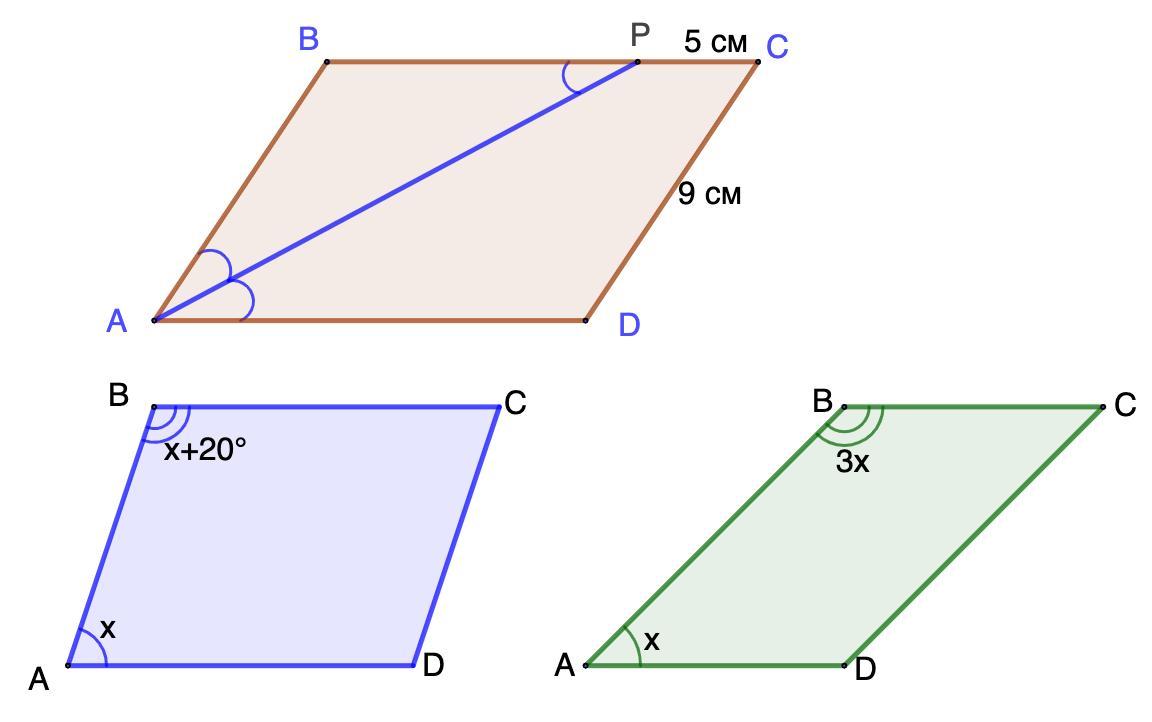
1. У паралелограмі ABCD AP-бісектриса. PC = 5 см, DC = 9см. Знайти периметр паралелограма ABCD.
2. ABCD- паралелограм
∆ А менший за ∆ В на 20.
Знайти кути паралелограма АBCD
3. АВCD- паралелограм
∆А менший за ∆ В у три рази.
Знайти кути паралелограма ABCD.
Допоможіть будь ласка
Ответы
Ответ:
1. Периметр равен 46 см;
2. ∠A = ∠C = 80°; ∠B = ∠D = 100°
3. ∠A = ∠C = 45°; ∠B = ∠D = 135°
Объяснение:
1. В параллелограмме ABCD AP-биссектриса. PC = 5 см, DC = 9 см. Найти периметр параллелограмма ABCD.
2. ABCD - параллелограмм. ∠А меньше ∠В на 20°.
Найти углы параллелограмма АBCD
3. АВCD - параллелограмм. ∠А меньше ∠В в три раза.
Найти углы параллелограмма ABCD.
1. Дано: ABCD - параллелограмм;
AP-биссектриса.
PC = 5 см, DC = 9 см.
Найти: Р(ABCD)
Решение:
Рассмотрим ABCD - параллелограмм.
- Противоположные стороны параллелограмма равны.
⇒ CD = AB = 9 см.
Рассмотрим ΔАВР.
∠ВАР = ∠РАD (AP-биссектриса)
∠APB = ∠РАD (накрест лежащие при ВС || AD и секущей АР)
⇒ ∠ВАР = ∠APB
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ АВ = ВР = 9 см
Тогда ВС = AD = 9 + 5 = 14 (см)
- Периметр параллелограмма равен удвоенной сумме смежных сторон.
Р(ABCD) = 2(AB + BC) = 2(9 + 14) = 46 (см)
2. Дано: ABCD - параллелограмм.
∠А меньше ∠В на 20°
Найти: углы параллелограмма.
Решение:
- Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Пусть ∠А = х, тогда ∠В = х + 20°.
∠А + ∠В = х + х + 20° = 180°
2х + 20° = 180°
2х = 160° |:2
х = 80°
∠А = 80°; ∠В = 80° + 20° = 100°
- Противоположные углы параллелограмма равны.
⇒ ∠A = ∠C = 80°; ∠B = ∠D = 100°
3. Дано: ABCD - параллелограмм.
∠А меньше ∠В в 3 раза
Найти: углы параллелограмма.
Решение:
Пусть ∠А = х, тогда ∠В = 3х
∠А + ∠В = х + 3х = 180°
4х = 180° |:4
х = 45°
∠А = 45°; ∠В = 45° · 3 = 135°
⇒ ∠A = ∠C = 45°; ∠B = ∠D = 135°