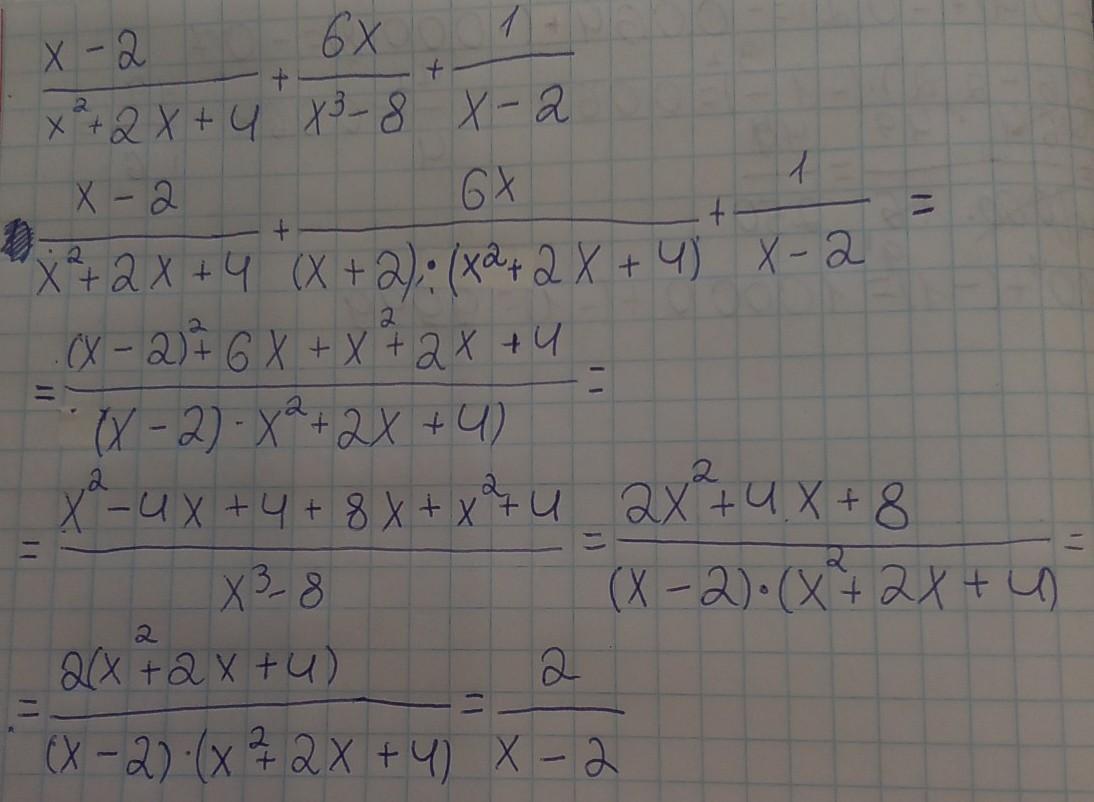(x - 2)/(x ^ 2 + 2x + 4) + (6x)/(x ^ 3 - 8) + 1/(x - 2) пж
Ответы
Формулы:
Разность кубов:
a³ - b³ = (a - b) · (a² + ab + b²)
Квадрат разности:
(a - b)² = a² - 2ab + b²
Решение:
[x - 2] / [x² + 2x + 4] + 6x / [x³ - 8] + 1 / [x - 2] =
= [x - 2] / [x² + 2x + 4] + 6x / [(x - 2) · (x² + 2x + 4)] + 1 / [x - 2] =
= [(x - 2)² + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)] =
= [x² - 4x + 4 + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)] =
= [2x² + 4x + 8] / [(x - 2) · (x² + 2x + 4)] =
= [2 · (x² + 2x + 4)] / [(x - 2) · (x² + 2x + 4)] = 2 / [x - 2]
Объяснение:
Раскладываем знаменатель второй дроби на множители по формуле разности кубов:
[x - 2] / [x² + 2x + 4] + 6x / [x³ - 8] + 1 / [x - 2] =
= [x - 2] / [x² + 2x + 4] + 6x / [x³ - 2³] + 1 / [x - 2] =
= [x - 2] / [x² + 2x + 4] + 6x / [(x - 2) · (x² + 2x + 4)] + 1 / [x - 2]
Приводим дроби к общему знаменателю:
[x - 2] / [x² + 2x + 4] + 6x / [(x - 2) · (x² + 2x + 4)] + 1 / [x - 2] =
= [(x - 2) · (x - 2) + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)] =
= [(x - 2)² + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)]
Раскрываем скобки в числителе дроби по формуле квадрата разности:
[(x - 2)² + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)] =
= [x² - 2 · 2x + 2² + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)] =
= [x² - 4x + 4 + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)]
Приводим подобные слагаемые:
[x² - 4x + 4 + 6x + x² + 2x + 4] / [(x - 2) · (x² + 2x + 4)] =
= [(1 + 1) · x² + (- 4 + 6 + 2) · x + 4 + 4] / [(x - 2) · (x² + 2x + 4)] =
= [2x² + 4x + 8] / [(x - 2) · (x² + 2x + 4)]
Раскладываем числитель дроби на множители (выносим 2 за скобки):
[2x² + 4x + 8] / [(x - 2) · (x² + 2x + 4)] =
= [2 · (x² + 2x + 4)] / [(x - 2) · (x² + 2x + 4)]
Сокращаем дробь на x² + 2x + 4:
[2 · (x² + 2x + 4)] / [(x - 2) · (x² + 2x + 4)] = 2 / [x - 2]
Ответ: 2 / [x - 2]
Ответ:
хорошей оценки)))
Объяснение:
:-(*(-*(-*(-_(