Предмет: Математика,
автор: passwo929394
математика пожалуйста , Розвязание , миллион баллов
Приложения:
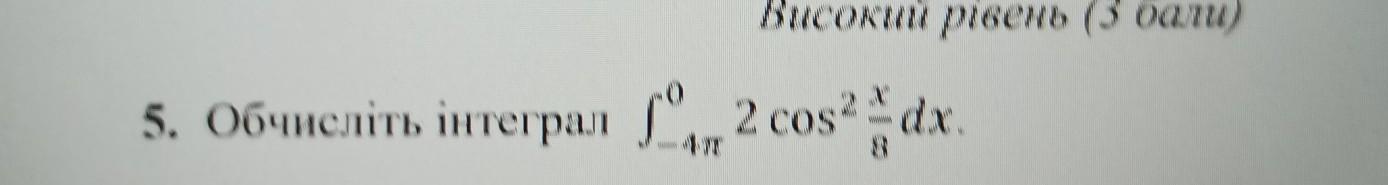
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Вычислите интеграл :
Воспользуемся формулой понижения степени
Подставим в интеграл
Выйдет :
Похожие вопросы
Предмет: Астрономия,
автор: markboroda30009
Предмет: Қазақ тiлi,
автор: hty9jcgpn4
Предмет: Биология,
автор: despinaklasssango
Предмет: Алгебра,
автор: mazizik
Предмет: Математика,
автор: erhov05092007