Предмет: Геометрия,
автор: milamarnis
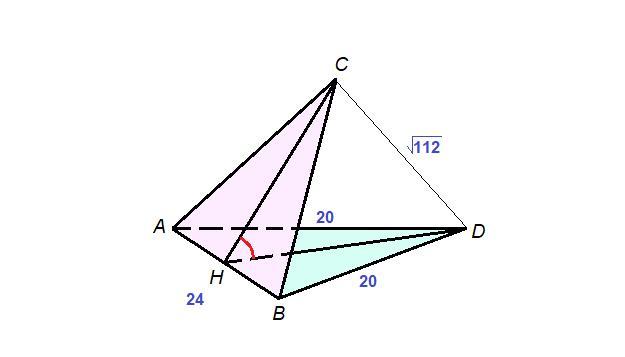
Рівносторонній трикутник ABC та рівнобедрений трикутник ABD не лежать в одній площині. Знайти двогранний кут з ребром AB , якщо AD=BD=20см , CD= корінь112см , AB=24см
KuOV:
Ошибка в условии, CD должно быть меньше 28.
испрпавила, там корень из 112
Ответы
Автор ответа:
2
Ответ:
Двугранный угол с ребром АВ равен 30°.
Объяснение:
Пусть Н - середина АВ, тогда DH⊥АВ как медиана и высота равнобедренного треугольника ABD, СН⊥АВ как медиана и высота равностороннего треугольника АВС.
DH⊥АВ, СН⊥АВ, значит
∠CHD - линейный угол двугранного угла между плоскостями треугольников - искомый.
см как высота равностороннего треугольника.
ВН = 0,5 АВ = 12 см
Из прямоугольного треугольника DHB по теореме Пифагора:
см
Из треугольника CHD по теореме косинусов:
∠CHD = 30°
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: darinaxwq
Предмет: История,
автор: Pomogitimnie
Предмет: Литература,
автор: aghjsnnsns
Предмет: Математика,
автор: yulyabedanova