Question

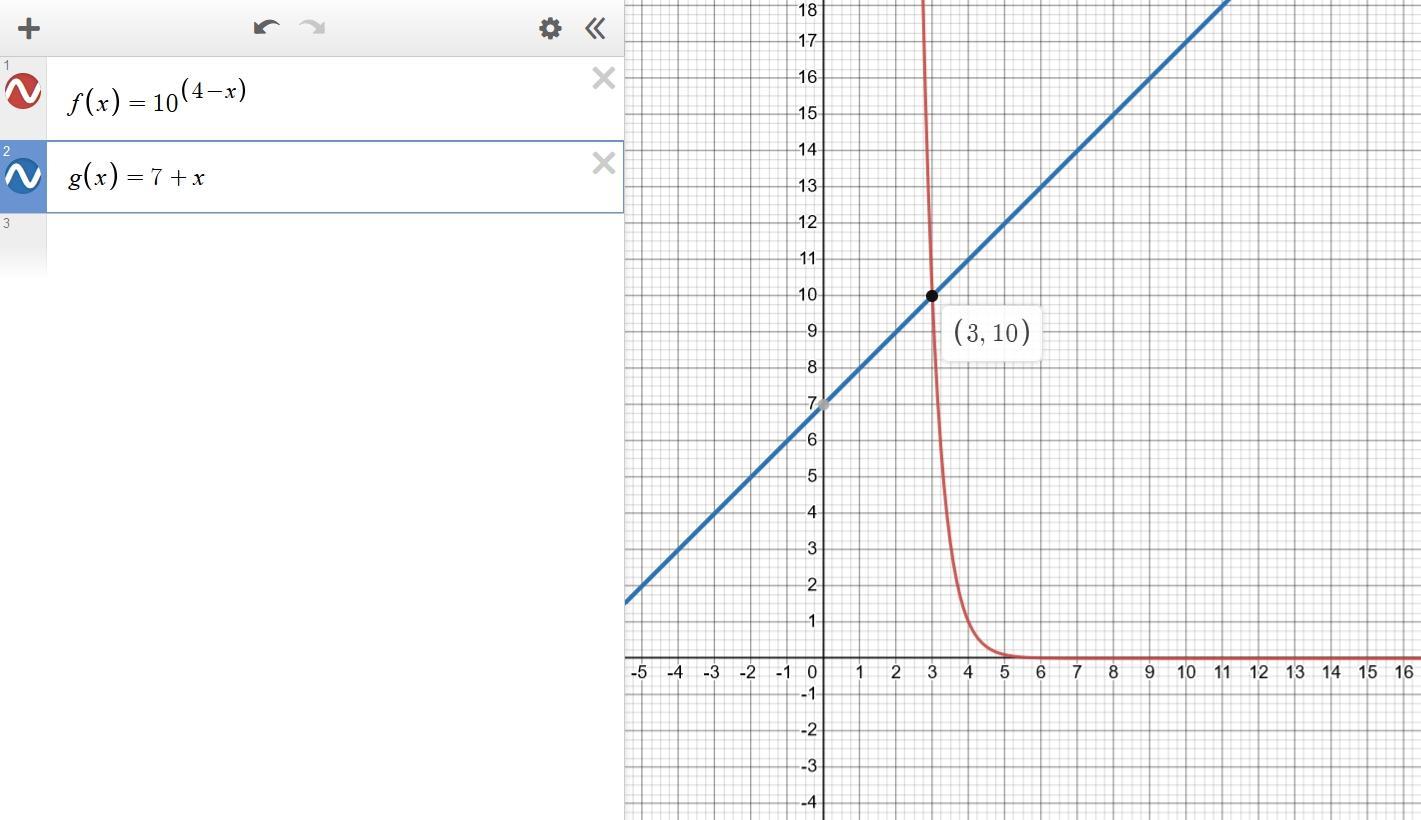
10^(4-x)>7+x
11 класс

Answer 1

$10^{4-x} > 7+x$

Исследуем функции, стоящие в обеих частях неравенства$f(x)=10^{4-x}\\f'(x)=10^{4-x} \ln 10 \cdot (-1)=-10^{4-x}\ln 10$.

Показательная функция $10^{4-x}$ всегда положительна, логарифм положителен, а значит, производная всегда отрицательна (в силу знака минус вначале), а значит, функция f(x) монотонно убывает.

$g(x)=7+x\\g'(x)=1$

Функция g(x) монотонно возрастает.

Получили, что одна функция монотонно убывает, а вторая возрастает, а значит, они имеют не более одной точки пересечения.

Находим её подбором — x=3:

$10^{4-3}=7+3$

Следовательно, x<3 (если сомневаешься, какой знак поставить, проверь каким-то значением, например x=1).

Ответ: x<3.

Чертёж приложен к ответу.