Предмет: Математика,
автор: mm7x8c8gz5
Помогите пожалуйста решить
Приложения:
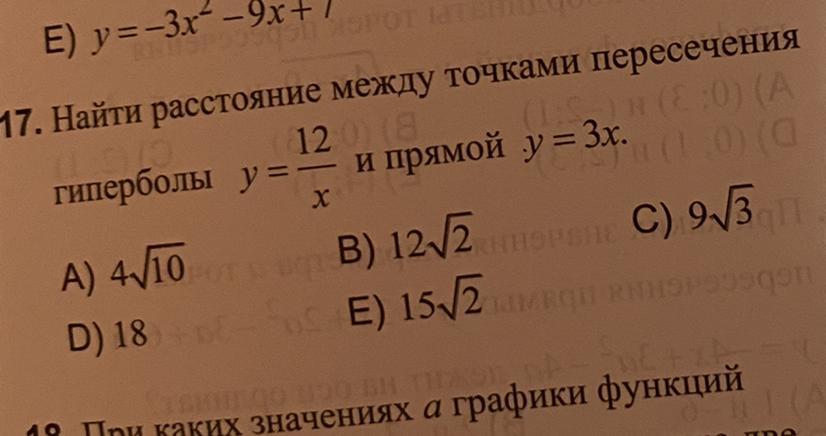
Ответы
Автор ответа:
0
Ответ:
Расстояние между точками пересечения равно 4√10.
Ответ: А)
Пошаговое объяснение:
17. Найти расстояние между точками пересечения гиперболы и прямой у = 3x
A) 4√10 B) 12√2 C) 9√3 D) 18 E) 15√2
Чтобы найти расстояние между точками пересечения, надо найти координаты этих точек пересечения.
Для этого решим систему:
- Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю.
12 - 3х² = 0
3(4 - х²) = 0
3(2 - х)(2 + х) = 0
х₁ = 2; х₂ = -2
Подставим значение х в любое из уравнений и найдем у:
у₁ = 6; у₂ = -6
Получили две точки пересечения: А(2; 6); В(-2; -6)
Теперь необходимо найти расстояние АВ:
nohopo880:
помогите с алгеброй,прошу!!!! буду очень благодарна!!!!
Похожие вопросы
Предмет: Українська мова,
автор: maksivanov4634
Предмет: Английский язык,
автор: foolelina46
Предмет: Математика,
автор: m36247005
Предмет: История,
автор: irina8378
Предмет: Математика,
автор: artemmironovic635