Предмет: Математика,
автор: adddaa001
Помогите решить задачу. Lim
Высшая математика
Приложения:
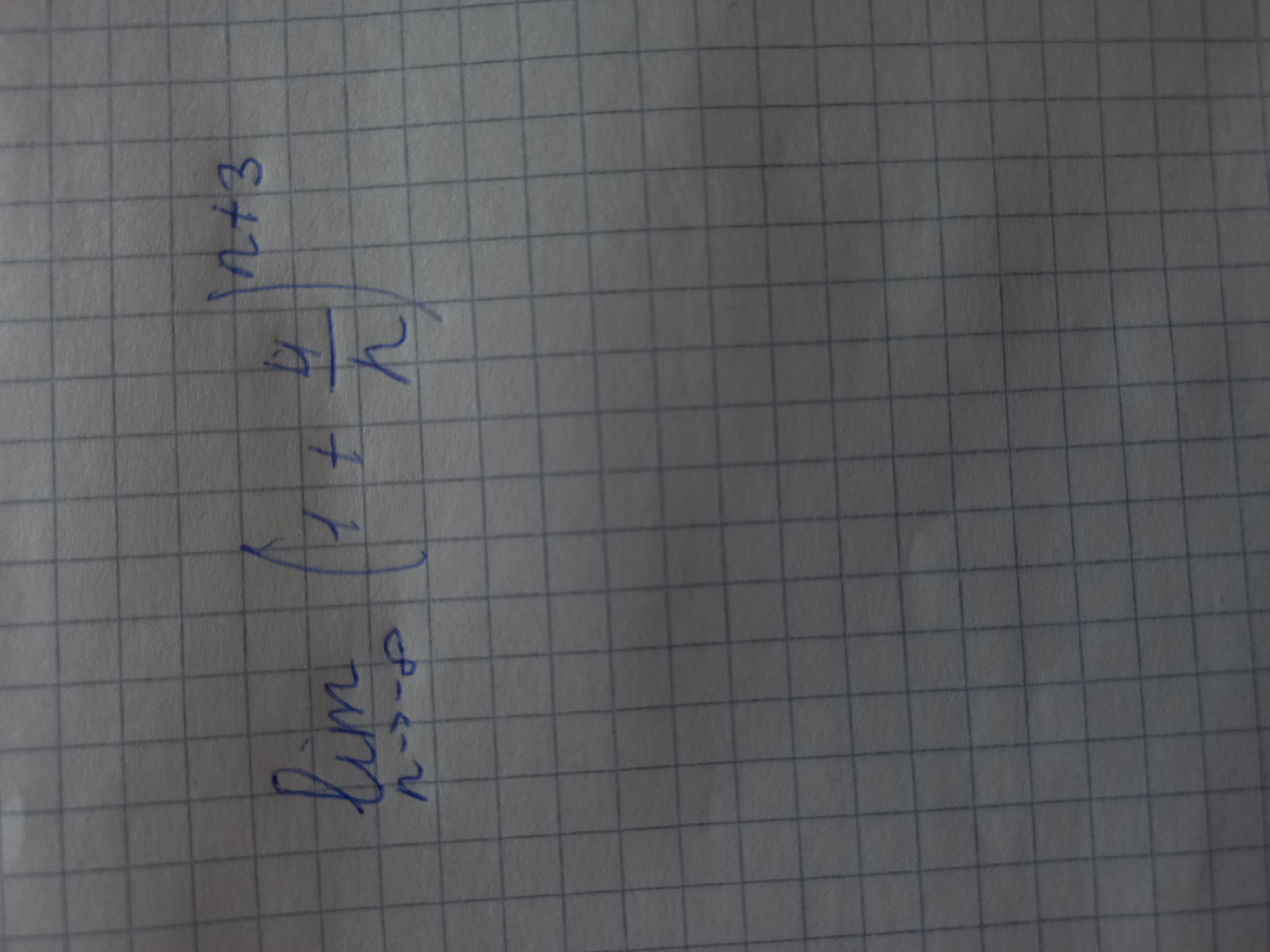
Ответы
Автор ответа:
0
Ответ:
Вычисление предела:
(limn→8(1+4/n))^limn→8(n+3)
limn→a(f(n)+g(n))=(limn→af(n))+(limn→ag(n))
f(n)=1
g(n)=4/n
(limn→81)+(limn→84/n))^limn→8(n+3)
limn→aC=C
limn→81=1
(1+(limn→84/n))^limn→8(n+3)
limn→8Cf(n)=C(limn→8f(n))
limn→84/n=4*(limn→81/n)
(1+4(limn→81/n))^limn→8(n+3)
limn→an^n=(limn→an)^n
(1+4/limn→8n)^limn→8(n+3)
limn→an=a
(1/2)^limn→8(n+3)
limn→a(f(n)+g(n))=(limn→af(n))+(limn→ag(n))
f(n)=n
g(n)=3
(1/2)^^^(limn→8^n)+(limn→8³)
lima→aC=C
limn→83=3
(1/2)^^^(limn→8^n)+3
limn→an=a
32
График функции:
n=-8
Упрощение:
Таблица значений:
n=-8
n|(1+4/n)^^^n+3
-8.1|32.21631972
-8.01|32.02178957
-7.99|31.97817538
-7.9|31.78016687
Похожие вопросы
Предмет: Математика,
автор: kolovejdo
Предмет: Биология,
автор: dashaschool0905
Предмет: Алгебра,
автор: arturzemko2018
Предмет: Русский язык,
автор: aaaaaaaaa64
Предмет: Химия,
автор: vladbvr