Предмет: Алгебра,
автор: goh65123
36. Найти сумму корней (в градусах) уравнения 4cos2 2x +2(√3+1)cos2x+√3=0, принадлежащих отрезку [0; п]. TOUL LIM
Приложения:
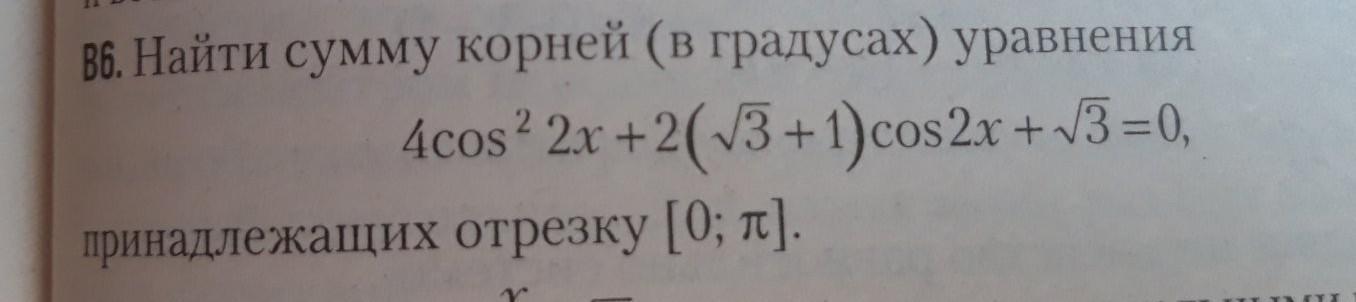
Ответы
Автор ответа:
0
cos(2x) + sin(2x) = cos(x)
2cos(x) + 2sin(x)cos(x) = cos(x)
cos(x) = 0 --> π/2 + πk
2cos(x) + 2sin(x) = 1
sin(x) + cos(x) = 1/2
√2sin(x + π/4) = 1/2
sin(x + π/4) = 1/2√2
x = 3π/4 - arcsin(1/2√2) +2πk
x = -π/4 + arcsin(1/2√2) +2πk
k - целое.
Корень, принадлежащий заданному интервалу: x= 0
2cos(x) + 2sin(x)cos(x) = cos(x)
cos(x) = 0 --> π/2 + πk
2cos(x) + 2sin(x) = 1
sin(x) + cos(x) = 1/2
√2sin(x + π/4) = 1/2
sin(x + π/4) = 1/2√2
x = 3π/4 - arcsin(1/2√2) +2πk
x = -π/4 + arcsin(1/2√2) +2πk
k - целое.
Корень, принадлежащий заданному интервалу: x= 0
Похожие вопросы
Предмет: Русский язык,
автор: Лиза25911
Предмет: Русский язык,
автор: marjona319
Предмет: Английский язык,
автор: олеся447
Предмет: География,
автор: Jdhdkeuo
Предмет: Химия,
автор: Zeroqqn