Предмет: Алгебра,
автор: alinnnka1
Срочно пожалуйста 50 баллов ❗❗❗❗❗❗❗❗❗❗❗❗❗❗❗❗❗❗ решите пожалуйста способом алгебраического сложения систему Ху=1/8 2х²+2у²=5/8
Ответы
Автор ответа:
1
Ответ:
Умножим на 2 первое уравнение и прибавим ко второму уравнению
и применим формулу квадрата суммы: .
Приложения:

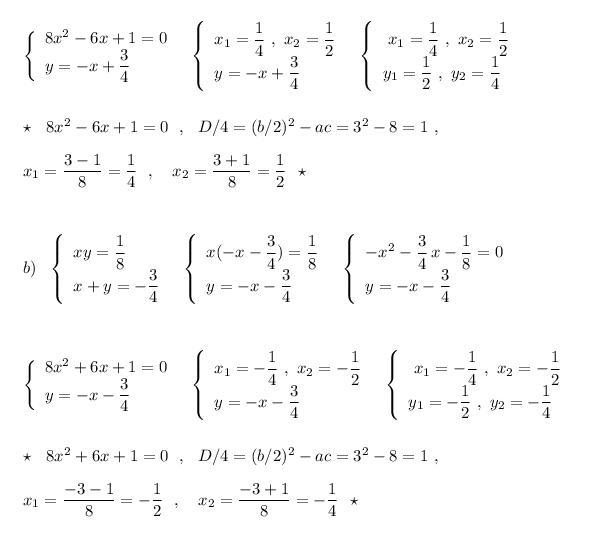
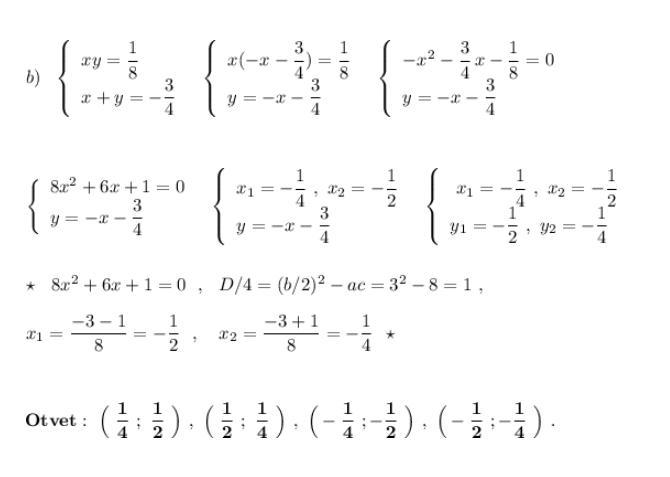
NNNLLL54:
сейчас скрин сброшу
смотри
а решение под А и Б это что ?
а это решение никак нельзя по другому сделать?
и это получается решение методом алгебраического сложения?
да, в самом начале сложили два уравнения, одно из которых умножено на 2 ... А дальше посложнее
почитай в учебнике, что такое метод алгебраического сложения ...
и "спасибо" отмечай
а в каком моменте именно прибавили эти два уравнения?
в 4 системе , там написано это действие словами
Похожие вопросы
Предмет: Технология,
автор: Натали4578
Предмет: Русский язык,
автор: ulyasha1711уляша
Предмет: Окружающий мир,
автор: svetatatu
Предмет: Математика,
автор: nsttrsv03
Предмет: Математика,
автор: milena2046