Предмет: Геометрия,
автор: dkdkd81w77
Пожалуйста ,помогите
геометрия 10 класс
Приложения:

cos20093:
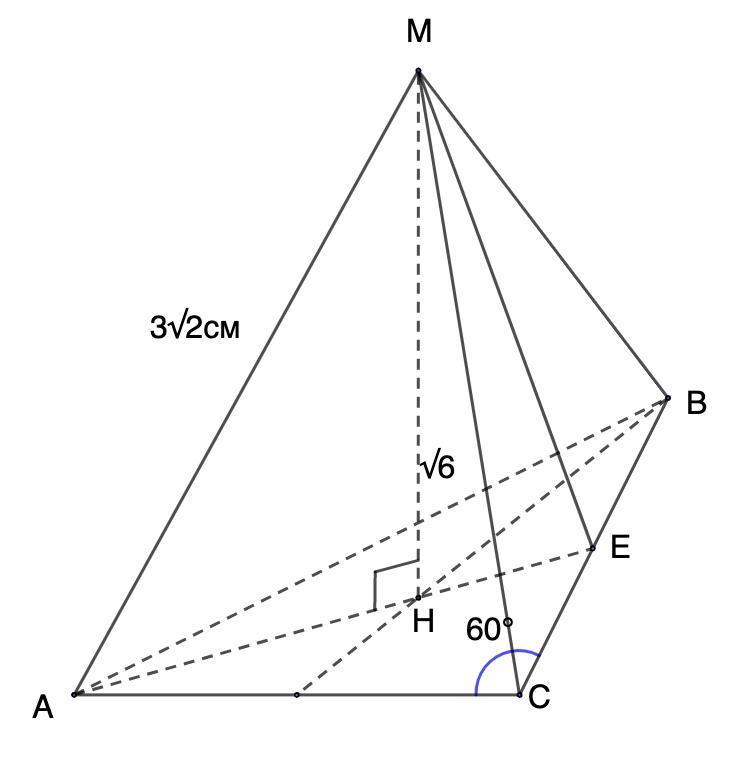
Ну, половина диагонали квадрата в основании HA = √12; если умножить на √2, найдется AB = 2√6. Все уже понятно, но я не могу удержаться от демонстрации "мелких трюков" - именно на них учатся (если конечно, хотят). Пусть середина AB - точка K. Для вычисления площади боковой поверхности надо найти MK. Легко заметить, что AK = √6, а в задаче уже был треугольник с таким катетом и гипотенузой MA (это MHA). То есть MK = HA = √12 = 2√3.
Но этот "ненужный" трюк содержит несколько больше, чем кажется. Легко понять, что Вся боковая поверхность состоит из 8 треугольников, равных MKA. А - внимание! - треугольник MAC (диагональное сечение) состоит из 2 таких треугольников. То есть нужная площадь равна 4 площадям MAC, S = 4*√6*√12.
Интересно, что заодно найден угол между плоскостями MAC и MAB, и он равен 60°. Это становится ясно в тот момент, когда обнаруживается равенство треугольников MKA и MHA, так как MHA - ортогональная проекция MAB на плоскость MAC, то есть косинус угла при проектировании равен 1/2
Ответы
Автор ответа:
0
Ответ:
Площадь боковой поверхности пирамиды равна 27 см².
Объяснение:
В правильной треугольной пирамиде MABC боковое ребро MA = 3√2 см, а высота пирамиды МН = √6 см. Найдите площадь боковой поверхности пирамиды.
Дано: МАВС - правильная пирамида;
MA = 3√2 см; МН = √6 см - высота;
Найти: Sбок
Решение:
- В правильной треугольной пирамиде основание - равносторонний треугольник, а грани - равные равнобедренные треугольники.
⇒ Sбок = 3 · S(СМВ)
- Площадь треугольника равна половине произведения основания на высоту.
⇒
1. Найдем МС.
- В равностороннем треугольнике все высоты являются медианами.
Рассмотрим ΔАМН - прямоугольный.
По теореме Пифагора найдем АН:
АН² = АМ² - МН² = 18 - 6 = 12
АН = √12 = 2√3 (см)
- Медианы треугольника пересекаются в одной точке и делятся в отношении 2 : 1, начиная от вершины.
⇒ НЕ = AH : 2 = 2√3 : 2 = √3 (см)
Тогда АЕ = 2√3 + √3 = 3√3 (см)
Рассмотрим ΔАЕС - прямоугольный.
- Углы в равностороннем треугольнике равны 60°.
⇒ ∠АСВ = 60°
- Синус угла - отношение противолежащего катета к гипотенузе.
2. Найдем апофему МЕ.
Рассмотрим ΔСМЕ - прямоугольный.
ΔСМВ - равнобедренный.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
⇒
По теореме Пифагора найдем МЕ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Слямгазин
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: ishmetova1988lmailru
Предмет: Геометрия,
автор: 3golovik
Предмет: Английский язык,
автор: Soplij