Question

В правильной четырехугольной пирамиде ABCDS с вершиной в точке S сто-
рона основания равна 24, боковое ребро равно 20. На ребра BS взята точка В так, что BS =5.Через точку В и середины ребер AS и CS проведена плоскость. Найдите угол между этой плоскостью и плоскостью основания пирамиды

Answer 1

Ответ:

∠LOB =arccos(3√2/5) ~31,95°

Объяснение:

Правильная четырехугольная пирамида - в основании квадрат, вершина падает в точку пересечения диагоналей. Диагонали квадрата перпендикулярны, равны, точкой пересечения делятся пополам.

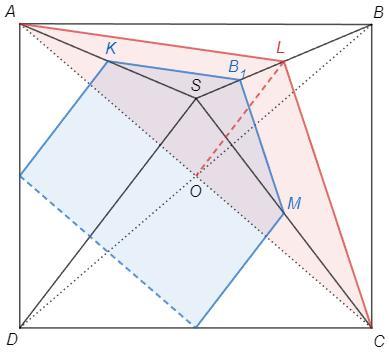
K, L, M - середины ребер AS, BS, CS

SL=10, B1S=5, B1 - середина SL => KB1 - средняя линия ASL, KB1||AL

Аналогично MB1||CL

Плоскость сечения KB1M параллельна плоскости ALC

∠LOB - угол между плоскостями (ALC) и (ABC) - искомый

LO - средняя линия SBD, LO||SD, ∠LOB=∠SDB

DO =CD/√2 =24/√2

cos(SDO) =DO/DS =24/20√2 =3√2/5