Предмет: Математика,
автор: kislovaelizaveta418
Найти все значения r при которых неравенство x^2-(2+r)×x+4>0 выполняется при всех действительных значениях x
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Условие задачи выполняется только если дискриминант данного квадратного трехчлена меньше нуля. Тогда все его значения имеют тот же знак, что и коэффициент при (в нашем случае это
).
То есть
Приложения:
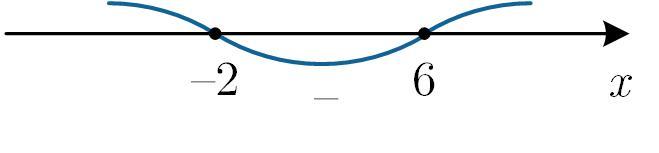
Похожие вопросы
Предмет: Английский язык,
автор: насколькобольше
Предмет: Русский язык,
автор: PaPavel08
Предмет: Русский язык,
автор: solomina87
Предмет: История,
автор: diana22886
Предмет: Математика,
автор: Аноним