Предмет: Геометрия,
автор: lalaasisusa
Помогите пожайлуста решить!
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
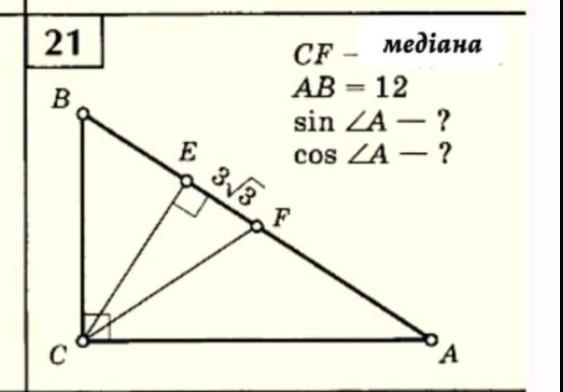
Если — медиана, то
,
По теореме Пифагора из треугольника
По теореме Пифагора из треугольника
Из метрических соотношений в треугольнике
Похожие вопросы
Предмет: Қазақ тiлi,
автор: СОСИСКАКЕК
Предмет: Русский язык,
автор: StupidChild1
Предмет: Другие предметы,
автор: Zalov23
Предмет: Информатика,
автор: fgdthjo
Предмет: Математика,
автор: syuzi1979