Предмет: Алгебра,
автор: norihonoremi
знайдіть f'(1), якщо f(x)=x⁵+√x
Ответы
Автор ответа:
2
Ответ:
5,5
Объяснение:
Тогда
Автор ответа:
2
Вітаю.
Розв'язання завдання додаю.
Приложения:
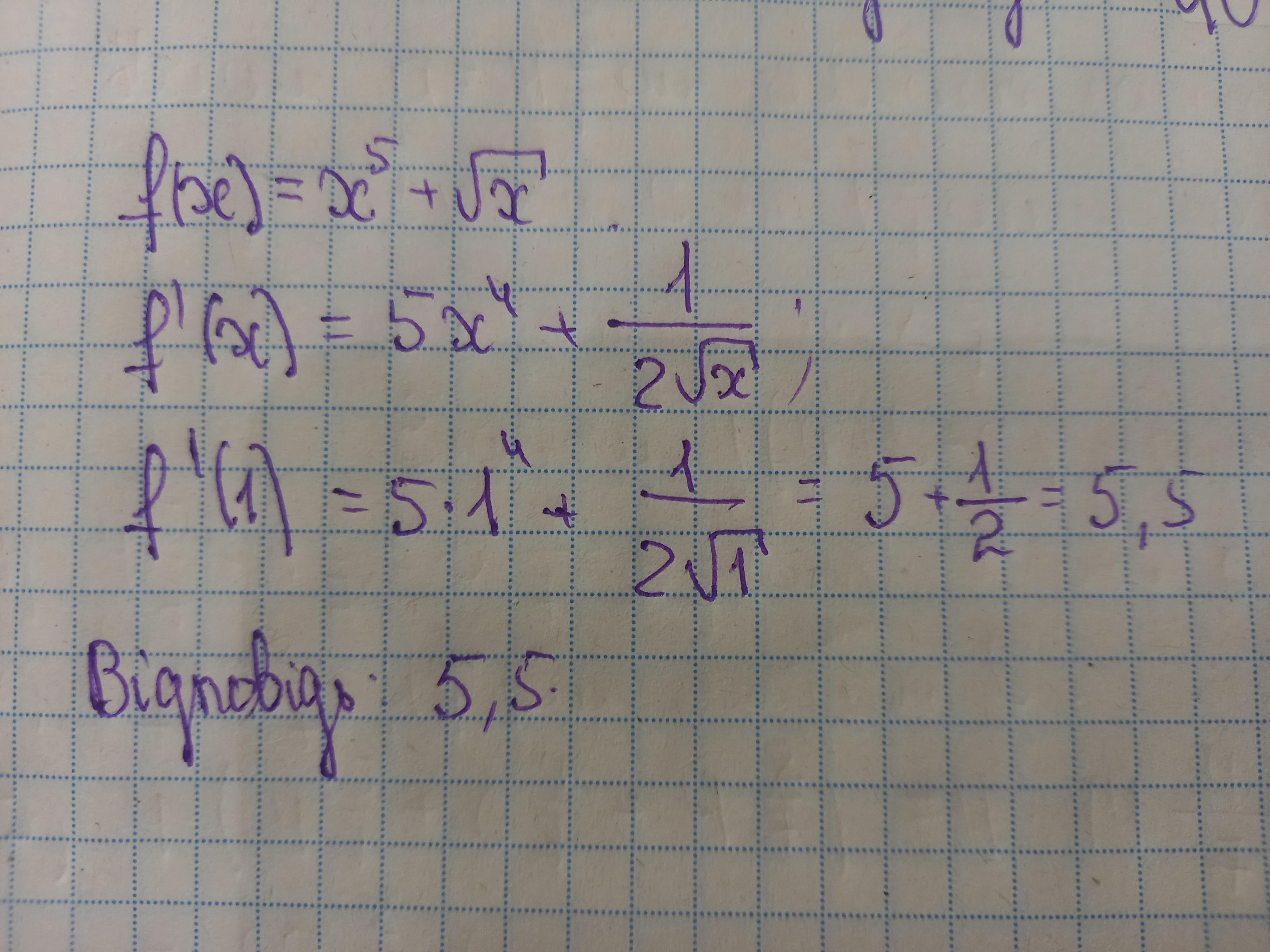

norihonoremi:
Алілуя відповідь не на російській
Похожие вопросы
Предмет: Русский язык,
автор: weter548
Предмет: Русский язык,
автор: ira1986
Предмет: Английский язык,
автор: sanyakyrgan
Предмет: Математика,
автор: 3763
Предмет: Математика,
автор: syuzi1979