Предмет: Математика,
автор: danikstavskiy
Математика 10 класс. Иррациональные уравнения
Приложения:
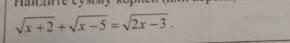
Ответы
Автор ответа:
2
Ответ:
Ответ: 5.
Пошаговое объяснение:
Решить иррациональное уравнение:
- Подкоренное выражение неотрицательно.
ОДЗ:
Возведем в квадрат обе части уравнения:
Оставим выражение с корнем слева, остальное перенесем вправо, не забывая поменять знак на противоположный, и приведем подобные члены:
- Произведение равно нулю, если хотя бы один из множителей равен нулю.
или
х₁ - посторонний корень, не входит в ОДЗ.
⇒ Ответ: 5.
Проверим:
Похожие вопросы
Предмет: Українська мова,
автор: олиджршджю
Предмет: Русский язык,
автор: pervii1
Предмет: Немецкий язык,
автор: mrSWAG
Предмет: Математика,
автор: ayka01217