Предмет: Алгебра,
автор: lysya2000
СРОЧНО!!! Нужно решить!!!
Приложения:
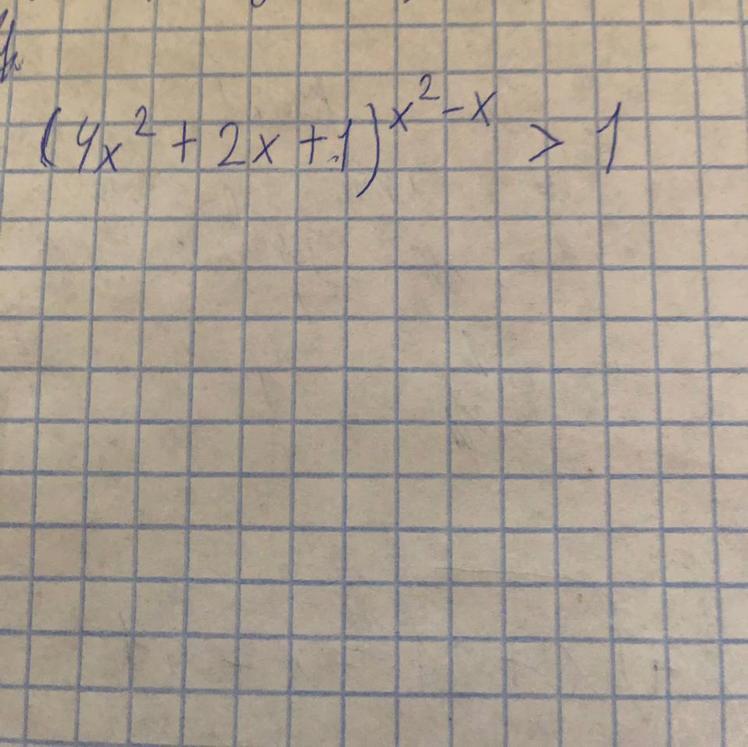
antonovm:
4x^2 +2x +1 > = 3/4 , неравенство определено при всех х и равносильно неравенству ( метод рационализации ) : ( x^2 -x )( 4x^2+2x) >0 ; x < - 0,5 или x > 1 ( ответ )
Ответы
Автор ответа:
0
Ответ:
Ограничения на показательно-степенную функцию:
Это неравенство верно при любых действительных х , так как дискриминант отрицателен: .
И .
Прологарифмируем неравенство.
Произведение двух множителей больше нуля, если эти множители имеют одинаковые знаки.
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Абу07
Предмет: Русский язык,
автор: kat2003058
Предмет: Қазақ тiлi,
автор: Ruf1001G
Предмет: История,
автор: berta1357