Предмет: Геометрия,
автор: kseniyaryazanova91
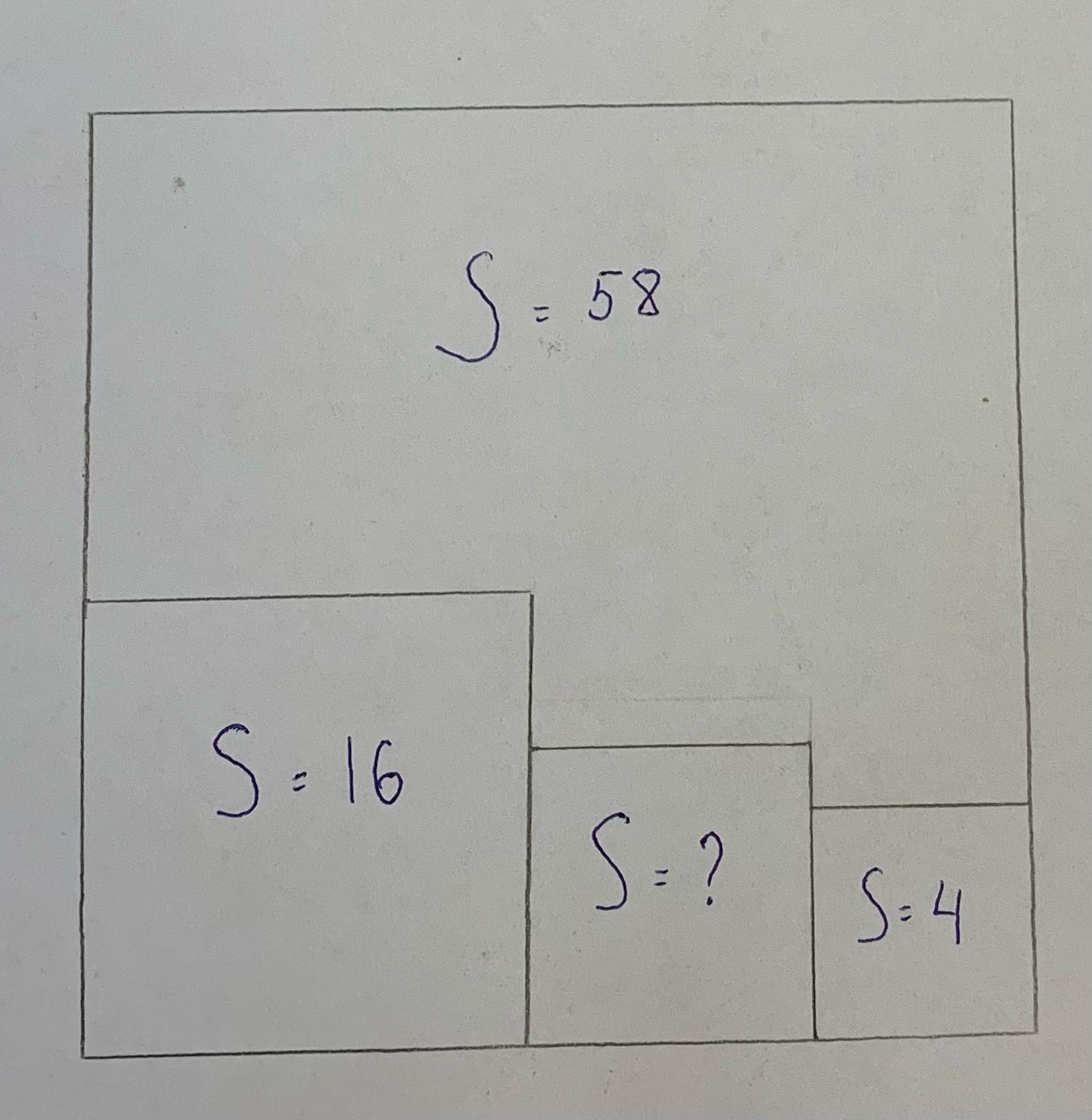
В квадрат вписаны три квадрата, по нижней стороне, от большего к меньшему. Известны площади: S = 58 (фигура без вписанных квадратов), S=16 (большой вписанный), S=4 (маленький вписанный). Найти площадь среднего вписанного квадрата.
Приложения:
Ответы
Автор ответа:
1
Объяснение:
обозначим:
площадь большого квадрата в который вписаны квадраты S .
S4=58
S1=16
S2=?
S3=4
cторона большего квадрата а
сторона a1=√S1=√16=4
сторона a2=√S2
сторона а3=√S3=√4=2
S=S1+S2+S3+S4
S=16+(a2)²+4+58=(a2)²+78
сторона а=а1+а2+а3=4+a2+2=
=6+a2
S=(6+(a2))²=36+12×a2+(a2)²
(a2)²+78=36+12(a2)+(a2)²
78-36=12(a2)
42=12(a2)
(a2)=42/12=7/2
S2=(a2)²=(7/2)²=49/4=12,25
ответ: S2=12,25
kseniyaryazanova91:
Дело в том, что S=58, это площадь не квадрата, там многоугольник. И вот так (a=√58) сторону а не найти.
в условии написано в КВАДРАТ вписано 3 квадрата
Да, но площадь основного большого квадрата, в который они вписаны не известна. 58 = это то что осталось после их добавления. На рисунке видно..
перерешала
Похожие вопросы
Предмет: Русский язык,
автор: kat2003058
Предмет: Қазақ тiлi,
автор: Ruf1001G
Предмет: Русский язык,
автор: АЛЁНА200603
Предмет: Химия,
автор: YarSmith
Предмет: География,
автор: AzizeIbragimova