Предмет: Математика,
автор: kropivkaa07
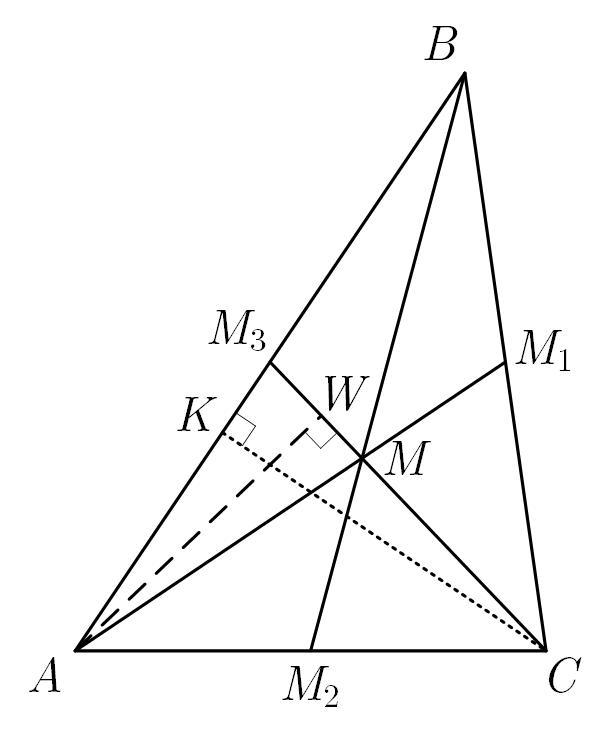
Доведіть, що медіани трикутника поділяють його на шість рівновеликих
трикутників
Ответы
Автор ответа:
1
Пошаговое объяснение:
Пусть ,
,
— медианы треугольника
,
— точка их пересечения. Как известно, каждая из медиан точкой их пересечения делится в отношении
, считая от вершины:
Отсюда, например,
Пусть площадь треугольника равна
. По формуле
можно записать:
Тогда
Значит медиана делит треугольник на два треугольника одинаковой площади (равновеликих треугольника).
Рассмотрим треугольник — один из шести треугольников, на которые разбивается треугольник
тремя медианами.
Его площадь
Аналогичные рассуждения можно провести и для пяти оставшихся треугольников.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: марина9931
Предмет: Русский язык,
автор: Kotuscha
Предмет: Окружающий мир,
автор: Кристинакошкина1
Предмет: Русский язык,
автор: leeeyyyi