Question

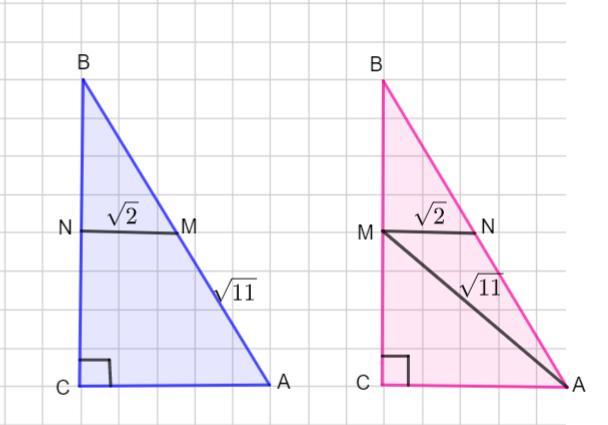
в прямоугольном треугольнике ABC с прямым углом C проведена средняя линия MN, параллельная катету AC. найдите длину BC, если AM = корень из 11, MN = корень из 2​

Answer 1

Ответ:

ВС = 6 ед. или ВС = 2√3 ед.  

Объяснение:

В прямоугольном треугольнике АВС с прямым углом С проведена средняя линия MN , параллельная катету АС . Найдите длину ВС , если АМ=√11, MN =√2

1 случай.

Пусть дан ΔАВС - прямоугольный.  Если MN - средняя линия, то М - середина гипотенузы АВ , N - середина катета ВС .

Если  АМ=√11 ед, то гипотенуза АВ=2√11 ед.

Средняя линия равна половине стороны, которой она параллельна. Тогда катет АС в 2 раза больше средней линии.

Если MN =√2 ед, то АС=2√2 ед.

Найдем катет ВС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB ^{2} =AC^{2} +BC^{2} ;\\BC^{2} =AB ^{2} -AC^{2};\\BC =\sqrt{AB ^{2} -AC^{2}} ;\\BC =\sqrt{(2\sqrt{11} )^{2}-(2\sqrt{2} )^{2} } =\sqrt{4\cdot11-4\cdot 2} =\sqrt{44-8} =\sqrt{36} =6$ ед.

Рассмотрим второй случай.

Точка М - середина катета ВС , N- середина гипотенузы АВ .

Если  MN - средняя линия, то катет  АС=2√2 ед. ( так как АС в 2 раза больше средней линии MN)

Рассмотрим Δ АСМ - прямоугольный и найдем катет МС по теореме Пифагора

$AM^{2} =AC^{2} +MC^{2} ;MC^{2} =AM^{2}-AC^{2};\\MC =\sqrt{AM^{2}-AC^{2}} ;\\MC = \sqrt{(\sqrt{11})^{2} -(2\sqrt{2})^{2} } =\sqrt{11-8} =\sqrt{3}$

Если М - середина катета ВС, то ВС в 2 раза больше длины отрезка МС.

ВС = 2√3 ед.