Предмет: Геометрия,
автор: Аноним
геометрия , очень срочно, помогите, дам лучший ответ
Приложения:
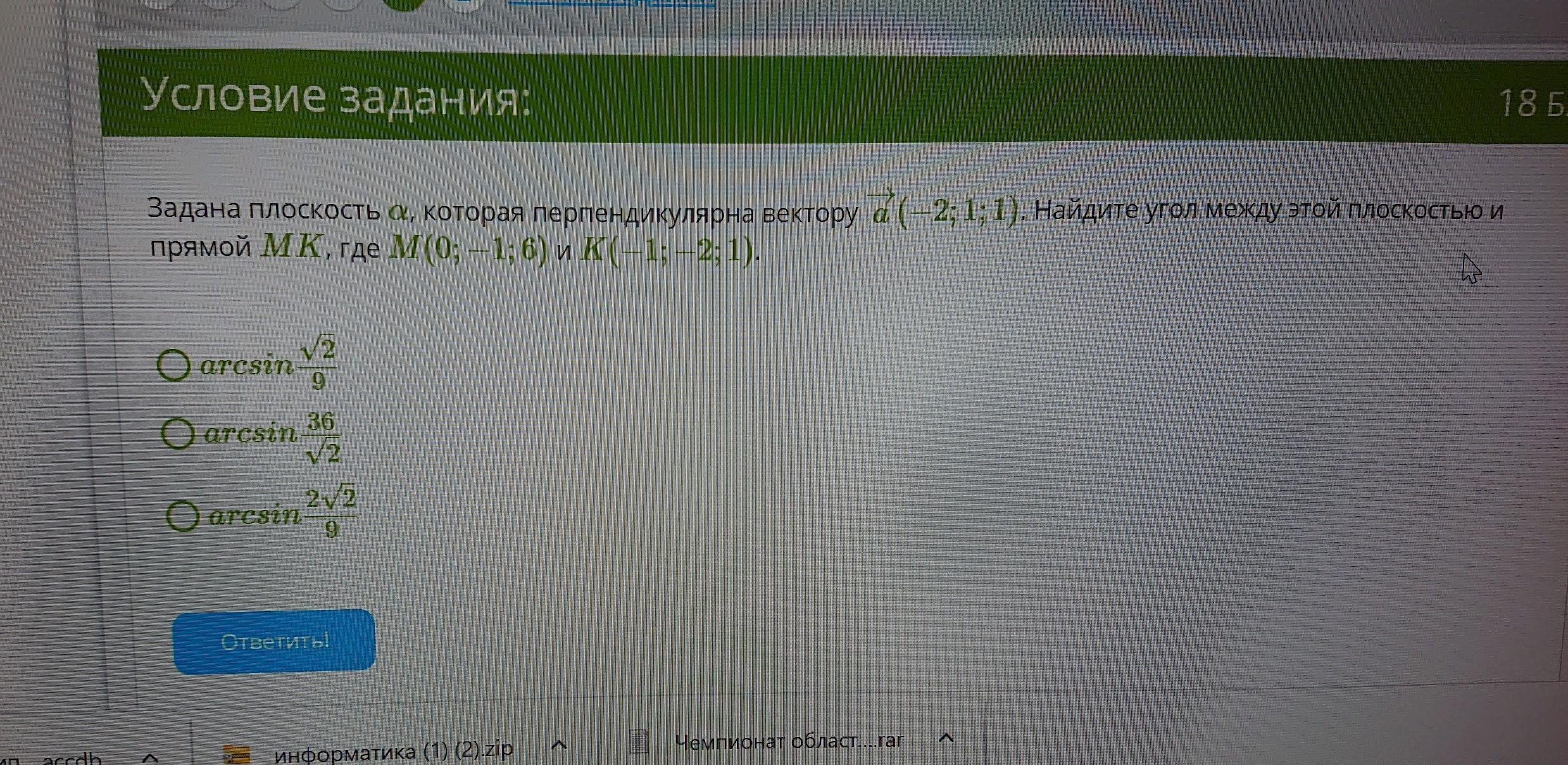
boretskyvladyslav:
3 правильне
Ваша
Ваша
Ваша
Ваша.а
Ваша
Ваша
Ваша.а
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Найдем координаты вектора
Если точки и
— начало и конец вектора, то координаты
Поэтому
Найдем угол между вектором и вектором нормали, перпендикулярным плоскости
По формуле скалярного произведения
Тогда
Вектор нормали перпендикулярен плоскости т. е. угол между ними равен
Значит угол между плоскостью и прямой равен
Так как
то
Похожие вопросы
Предмет: Русский язык,
автор: ladyket
Предмет: Английский язык,
автор: danil641
Предмет: Окружающий мир,
автор: YuliaAy2011
Предмет: Химия,
автор: maksat204yt
Предмет: Физика,
автор: emomnazarov03