помогите пожалуйста !!!
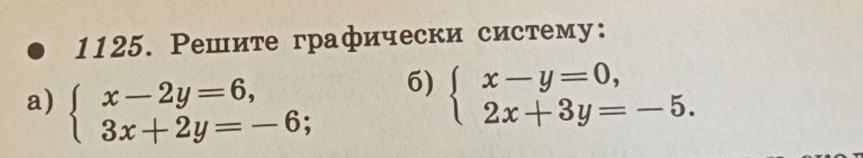
Ответы
1. {x-2y=6
{2y=-6-3x
x-(-6-3x)=6
x=0
2y=-6-3×0
y=-3
(x,y)=(0,-3)
{0-2×(-3 )=6
{3×0+2×(-3)=-6
{6=6
{-6=-6
(x,y)=(0, -3)
2.
{x=y
{2x+3x=-5
2y-3y=-5
y=-1
x=-1
(x,y)=(-1,-1)
{-1-(-1)=0
{2×(-1)+3×(-1)=-5
{0=0
{-5=-5
(x,y)=(-1,-1)
Ответ:
а) б)
Пошаговое объяснение:
а) Выразим из каждого уравнения системы через
:
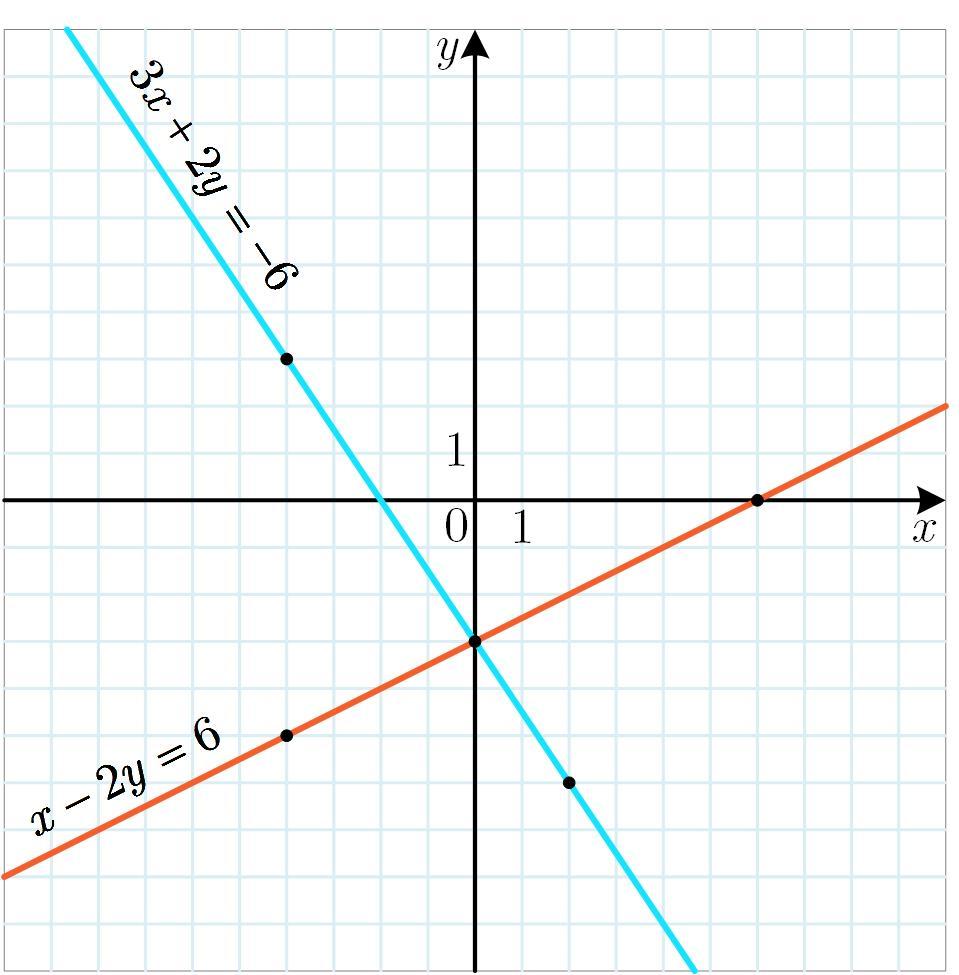
Каждое из уравнений имеет вид следовательно, задает прямую. Для построения прямой достаточно обозначить две точки, принадлежащие ей, и провести линию через них.
Для прямой выберем
тогда
и
тогда
Нанесем точки
и
на плоскость и проведем через них линию (обозначена оранжевым цветом).
Для прямой выберем
тогда
и
тогда
Нанесем точки
и
на плоскость и проведем через них линию (обозначена голубым цветом).
Эти прямые пересекаются в точке с координатами следовательно эта пара и является решением системы.
б) Выразим из каждого уравнения системы через
:
Каждое из уравнений имеет вид следовательно, задает прямую. Для построения прямой достаточно обозначить две точки, принадлежащие ей, и провести линию через них.
Для прямой выберем
тогда
и
тогда
Нанесем точки
и
на плоскость и проведем через них линию (обозначена сиреневым цветом).
Для прямой выберем
тогда
и
тогда
Нанесем точки
и
на плоскость и проведем через них линию (обозначена синим цветом).
Эти прямые пересекаются в точке с координатами следовательно эта пара и является решением системы.