Question

Помогите решить задачу, т.Пифагора​

Answer 1

Ответ:

x=3

Объяснение:

За опорним фактом катет, що лежить проти кута 30°, дорівнює половині гіпотенузи:

NS=MN/2=(2√3)/2=√3

За теоремою Піфагора:

MS=√(MN²-NS²)=√((2√3)²-(√3)²)=√(12-3)=√9=3

Answer 2

***

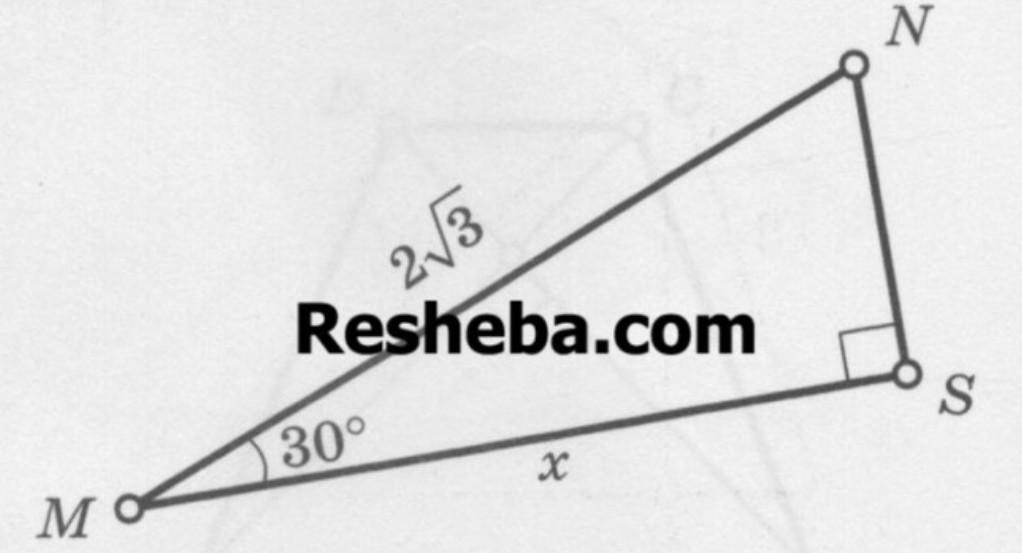
дано:

прямоугольный треугольник MSN

∠S = 90°

∠M = 30°

MN = 2√3

______________

MS = ?

решение:

находим сторону NS по теореме о катете, лежащем против угла 30°:

• катет прямоугольного треугольника, лежащий против угла 30° равен половине гипотенузы.

$NS =\frac{1}{2} MN=\frac{2\sqrt{3} }{2} = \sqrt{3}$

находим сторону MS по теореме Пифагора:

• сумма квадратов длин катетов равна квадрату длины гипотенузы  $c^2 = a^2+b^2$

$MN^2=MS^2+NS^2$

=>

$MS^2=MN^2-NS^2$

$MS^2=(2\sqrt{3})^2-(\sqrt{3} )^2=(2\cdot2 \cdot\sqrt{3} \cdot\sqrt{3} )-(\sqrt{3} \cdot\sqrt{3} )$

$MS^2= 12-3=9$

$MS =\sqrt{9} =3$

ответ: сторона MS (x) равна 3 (см).