Question

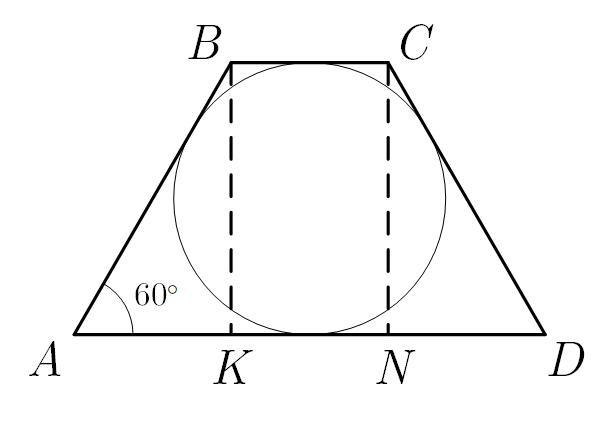
Площа рівнобічної трапеції, описаної навколо круга, дорівнює S. Знайти
бічну сторону трапеції, якщо гострий кут при основі дорівнює 60градусів.​

Answer 1

Ответ:

Боковая сторона трапеции равна $\sqrt[4]{{\frac{{4{S^2}}}{3}}}$

Объяснение:

Опустим высоты $BK$ и $CN$ на нижнее основание трапеции. Тогда прямоугольные треугольники $BKA$ и $CND$ равны.

Пусть боковая сторона трапеции $AB = CD = x$.  Из треугольника $BKA$ через метрические соотношения

$BK = x\sin 60^\circ = \displaystyle\frac{{\sqrt 3 }}{2}x.$

Условием того, что в четырехугольник можно вписать окружность, является равность сумм противоположных сторон. Значит $BC + AD = AB + CD = 2x$.

По формуле площади трапеции

$S = \displaystyle\frac{{AB + CD}}{2} \cdot BK = \displaystyle\frac{{2x}}{2} \cdot \displaystyle\frac{{\sqrt 3 }}{2}x = \displaystyle\frac{{\sqrt 3 }}{2}{x^2},$

откуда

${x^2} = \displaystyle\frac{{2S}}{{\sqrt 3 }};\\\\ x = \sqrt {\displaystyle\frac{{2S}}{{\sqrt 3 }}} = \sqrt[4]{{\displaystyle\frac{{4{S^2}}}{3}}}.$