Предмет: Алгебра,
автор: iliakuruch9
a) x⁴-x³-13x²+x+12=0
б) x⁴-x³-7x²+x+6=0
Ответы
Автор ответа:
0
Ответ:
1.) -3, -1, 1, 4
2.) -2, -1, 1, 3
Приложения:
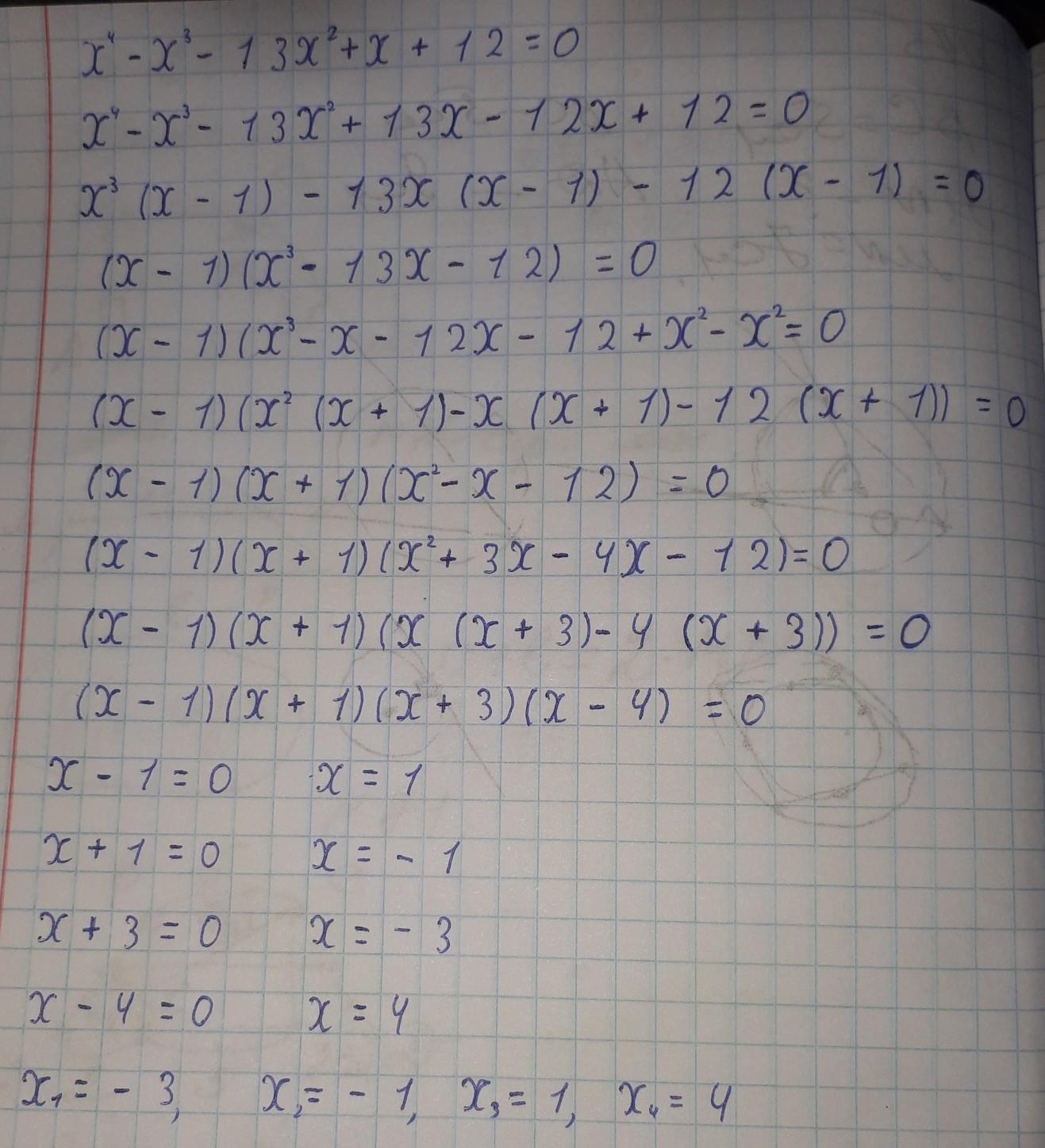
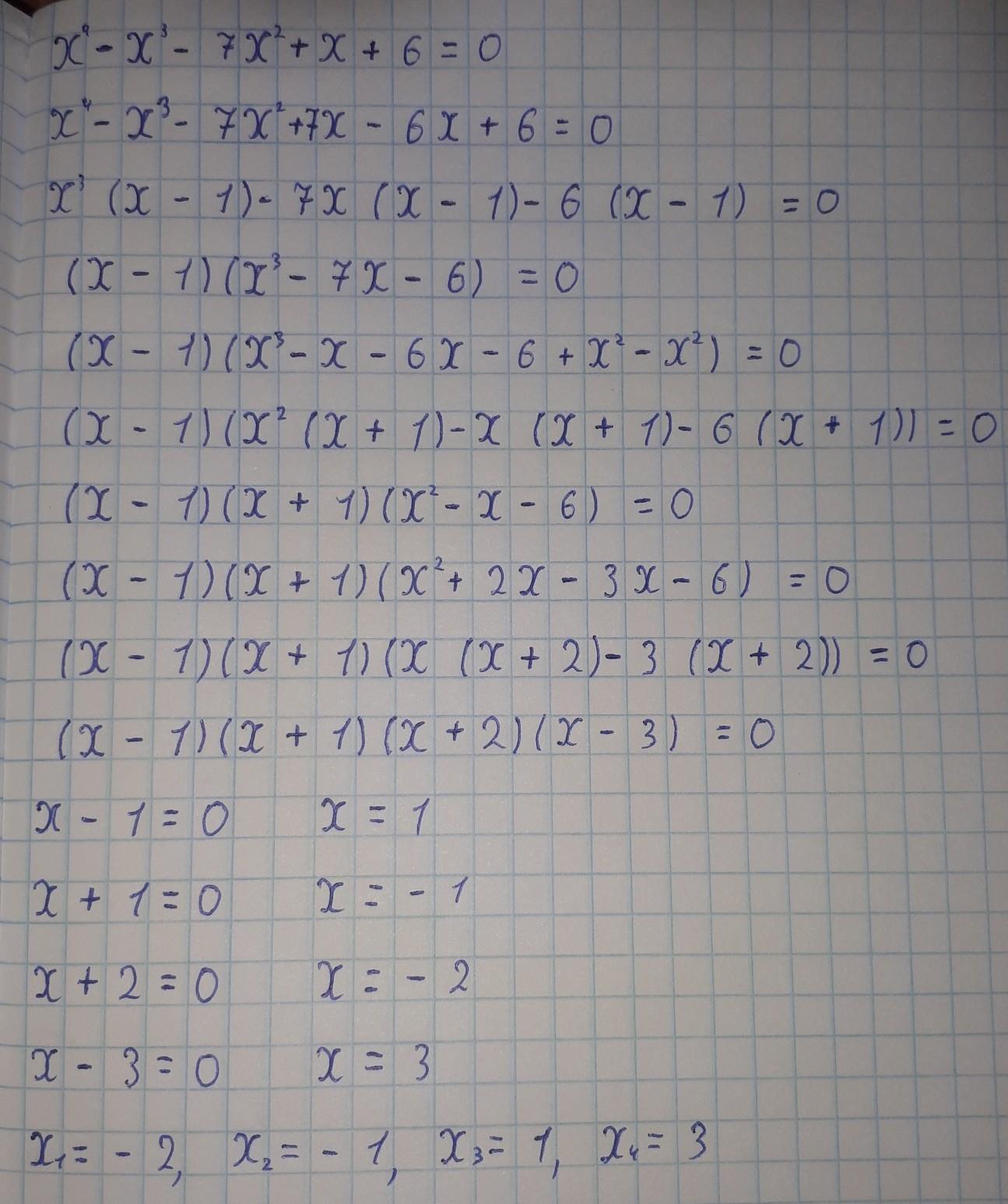
Автор ответа:
0
Ответ:
a) 1; - 1; 4; - 3; б) 1; - 1; 3; - 2
Объяснение:
Две однотипные задачи с легко угадываемыми корнями.
a)
б)
Похожие вопросы
Предмет: Английский язык,
автор: alisa218
Предмет: Русский язык,
автор: semen123321
Предмет: Русский язык,
автор: 12шох12
Предмет: Математика,
автор: compom
Предмет: Русский язык,
автор: malischka86