Предмет: Алгебра,
автор: financemnkiboyqy3e
69. Вычислите значение выражения ( простым способом!!!! )
Приложения:
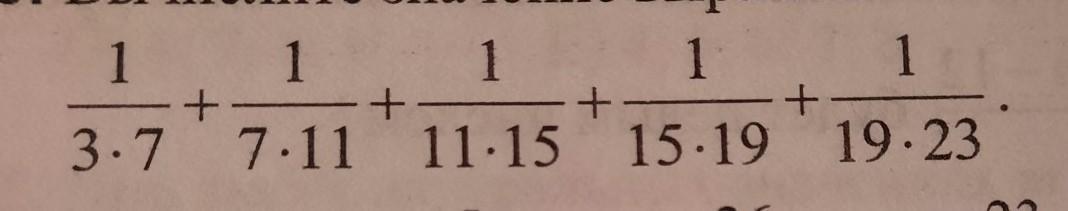
Ответы
Автор ответа:
2
Розв'язання ##########
Приложения:
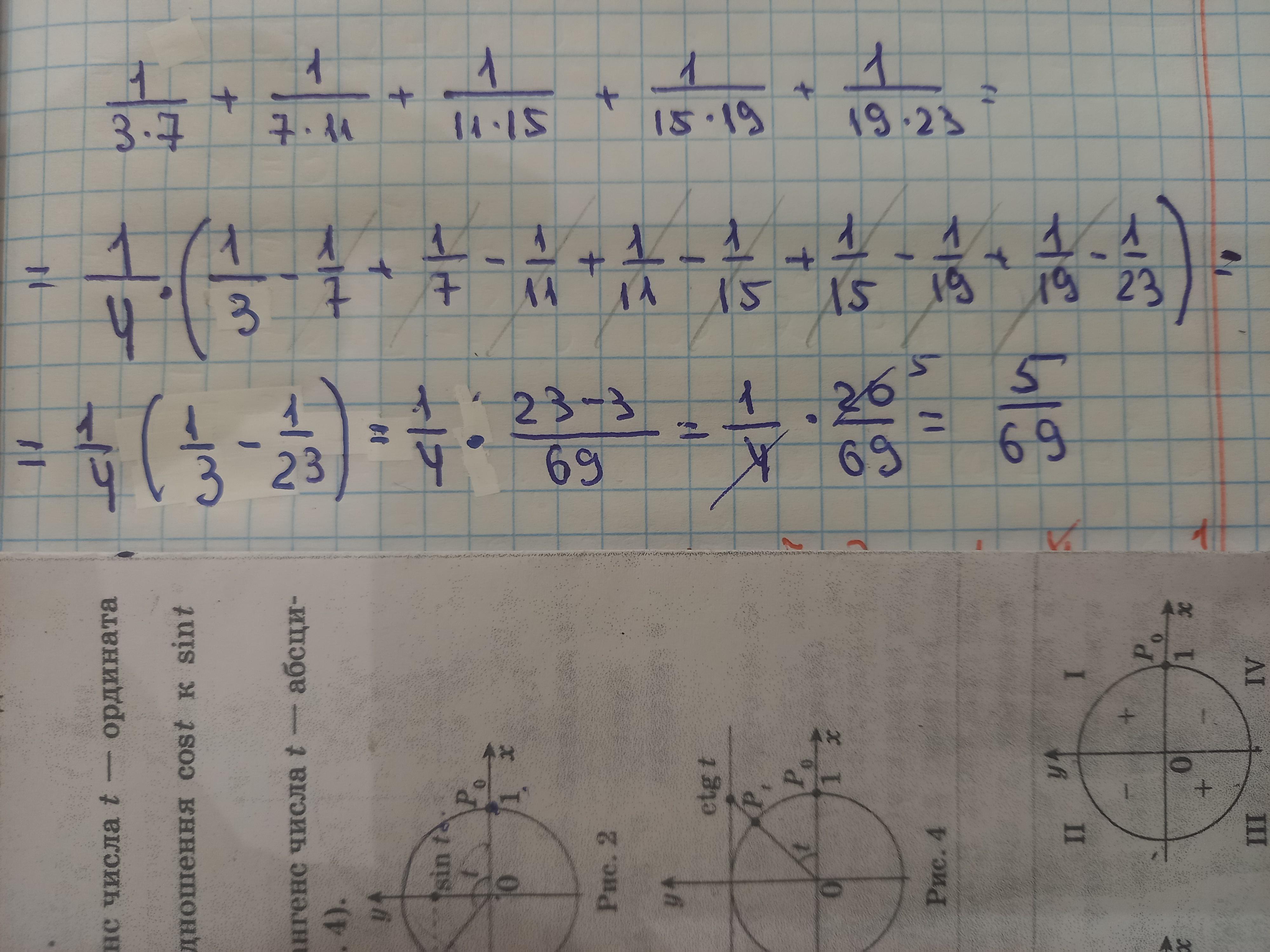
Автор ответа:
0
Ответ:
Заметим, что множители в знаменателе отличаются друг от друга на 4 . Поэтому выведем формулу:
Значит, .
Похожие вопросы
Предмет: Русский язык,
автор: ЛизаТеплинская
Предмет: Українська література,
автор: smail1220
Предмет: Українська мова,
автор: Dimon11960
Предмет: Биология,
автор: 1736dh
Предмет: Русский язык,
автор: anastasiya4661