Question

Срочно помогите плиз

Сторони кута А, що дорівнює 60°, дотикаються до кола. Знайдіть відстань від вершини кута А до центра кола, якщо радіус кола дорівнює 6 см.

Answer 1

Ответ:

Расстояние от вершины угла А до центра окружности равно 12 см

Объяснение:

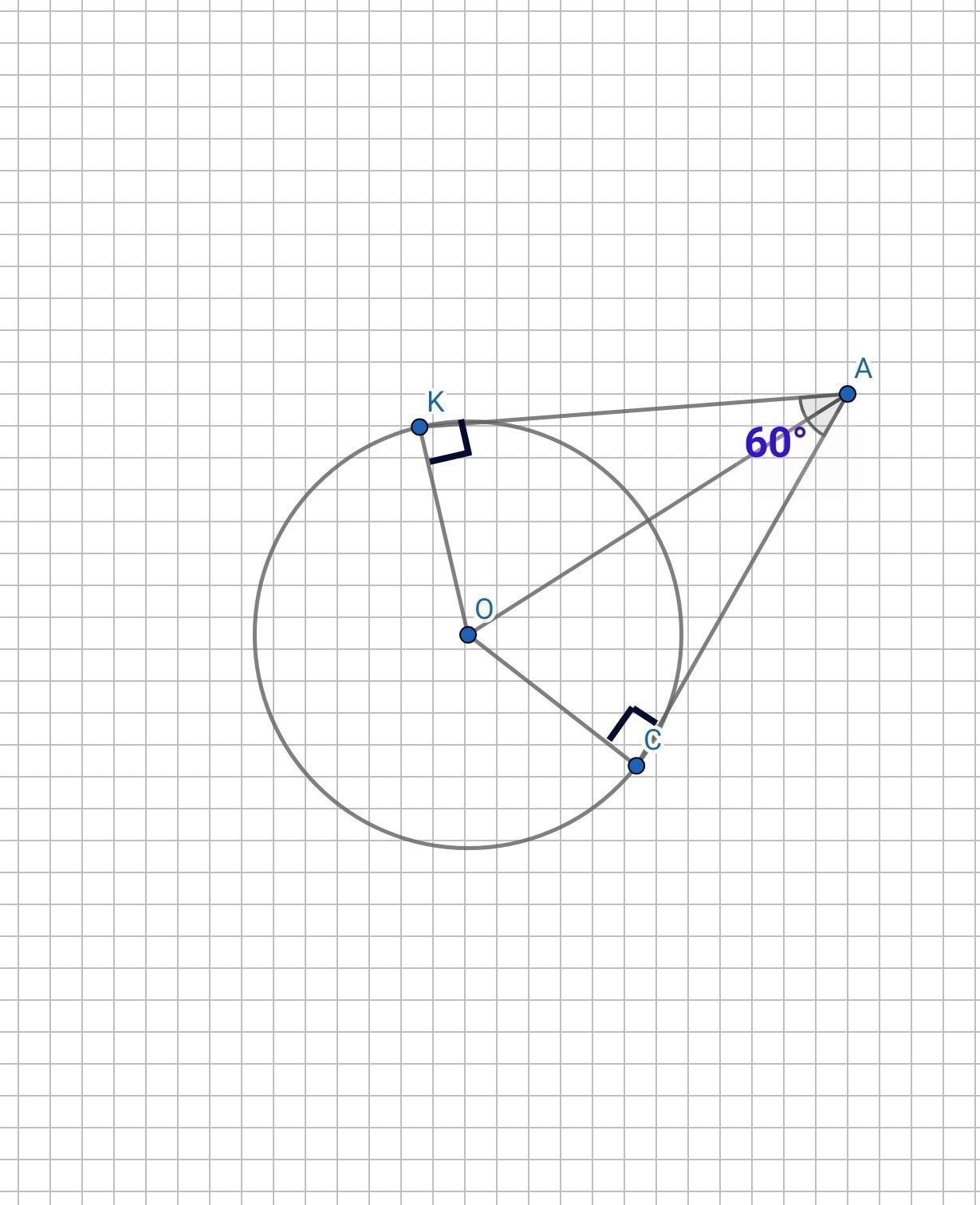
∠A=60°. АК и АC - касательные к окружности с центром в точке О. OK и OC - радиусы окружности, проведённые в точки касания. OK=OC=6см.

Найдём AO.

По свойству касательных к окружности:

1) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания

Следовательно AK⟂OK, AC⟂OC. △AKO и △ACO прямоугольные.

2) Отрезки касательных к окружности, проведённых из одной точки, составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Следовательно ∠OAK=∠OAC=∠A:2=60°:2=30°.

В прямоугольном треугольнике AKO, катет ОК лежит напротив угла в 30°, а значит он равен половине гипотенузы.

Следовательно гипотенуза АО=2•ОК=2•6=12 см.