Question

помогите с математикой

Answer 1

Ответ:

12. Периметр данного треугольника равен  (20 +12√5) см.

13. Диагонали ромба равны 10√29 см и 4√29 см.

14. Диаметр окружности равен 45 см.

Пошаговое объяснение:

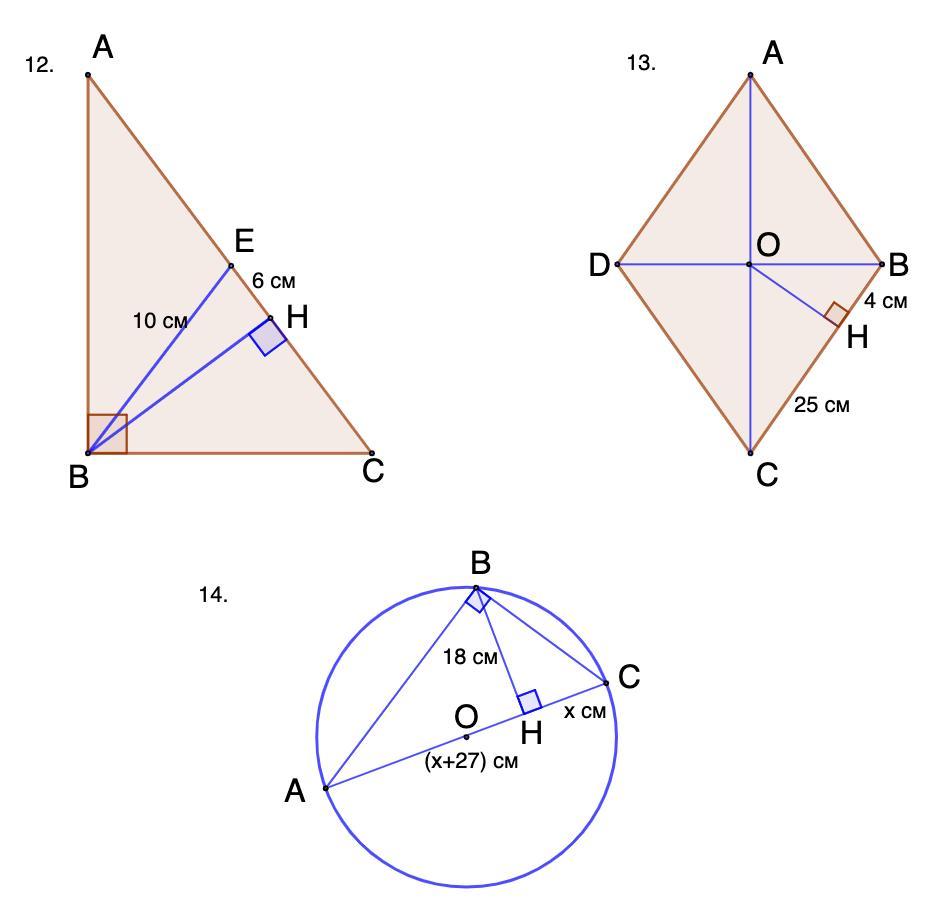
12. Медиана прямоугольного треугольника, проведенная к гипотенузе равна 10 см, а расстояние между серединой гипотенузы и основанием высоты треугольника, проведенной к гипотенузы, равно 6 см. Найдите периметр данного треугольника.

13. Перпендикуляр, проведенный из точки пересечения диагоналей ромба к его стороне, делит ее на отрезки длиной 4 см и 25 см. Найдите диагонали ромба.

14. Перпендикуляр, опущенный с точки окружности на его диаметр, делит диаметр на два отрезка, один из которых на 27 см больше второго. Найдите диаметр круга, если длина перпендикуляра равна 18 см.

Для решения данных задач воспользуемся метрическими соотношениями в прямоугольном треугольнике:

• Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

12. Дано: ΔАВС - прямоугольный;

ВЕ = 10 см - медиана;

ВН - высота;

ЕН = 6 см.

Найти: Р(АВС)

Решение:

Рассмотрим ΔАВС - прямоугольный.

• Медиана, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы.

⇒ ВЕ = АЕ = ЕС = 10 см.

Тогда АС = 20 см.

СН = ЕС - ЕН = 10 - 6 = 4 (см)

АН = АЕ + ЕН = 10 + 6 = 16 (см)

Воспользуемся метрическими соотношениями в прямоугольном треугольнике:

ВС² = СН · АС = 4· 20 = 80

ВС = √80 = 4√5 (см)

АВ² = АН · АС = 16 · 20 = 320

АВ = √320 = 8√5 (см)

• Периметр треугольника - сумма длин всех его сторон.

Р(АВС) = 20 + 4√5 + 8√5 = (20 +12√5) (см)

Периметр данного треугольника равен  (20 +12√5) см.

13. Дано: ABCD - ромб;

АС и BD - диагонали;

ОН ⊥ СВ;

НВ = 4 см; СН = 25 см.

Найти: BD и АС.

Решение:

Рассмотрим ΔСОВ.

• Диагонали ромба взаимно перпендикулярны.

⇒ ΔСОВ - прямоугольный.

ОС² = СН · СВ = 25 · (4 + 25) = 25 · 29

ОС = 5√29 см.

ОВ² = ВН · СВ = 4 · 29

ОВ = 2√29 см.

• Диагонали ромба точкой пересечения делятся пополам.

⇒ АС = 2 · ОС = 10√29 (см)

BD = 2 · OB = 4√29 (см)

Диагонали ромба равны 10√29 см и 4√29 см.

14. Дано: Окр.О;

АС - диаметр;

ВН ⊥ АС;

ВН = 18 см;

АН - НС = 27 см.

Найти: АС.

Решение:

Соединим А и С с В.

• Вписанный угол, опирающийся на диаметр, равен 90°.

⇒ ∠АВС = 90°.

Рассмотрим ΔАВС - прямоугольный.

Пусть НС = х см, тогда АН = (х + 27) см.

ВН² = НС · НА

324 = х(х + 27)

$\displaystyle \bf x^2 + 27x - 324 = 0\\\\D = 729 + 1296 = 2025\\\\\sqrt{D}=45\\ \\x_1=\frac{-27+45}{2}=9;\;\;\;\;\;x_2=\frac{-27-45}{2} =-36$

x₂ < 0 ⇒ посторонний корень.

НС = 9 (см);   АН = 9 + 27 = 36 (см)

⇒ АС = НС + АН = 9 + 39 = 45 (см)

Диаметр окружности равен 45 см.