Предмет: Алгебра,
автор: ellis0440
очень срочно пожалуйста
Приложения:

ВикаБач:
2)
Ответы
Автор ответа:
1
Ответ:
Ответ № 2
Объяснение:
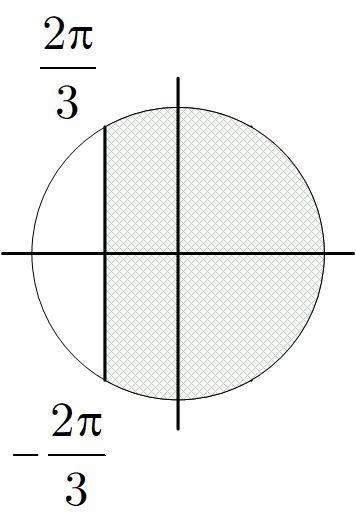
На единичной окружности линией отмечаем положение Тогда все точки окружности правее этой линии являются решениями данного неравенства.
Тогда
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: мая80
Предмет: Английский язык,
автор: СанкиSLOMALIS
Предмет: Русский язык,
автор: Ирлана4444
Предмет: Математика,
автор: sirin200312
Предмет: Українська література,
автор: misaplehanov83