Предмет: Алгебра,
автор: chillingmail
Подскажите откуда всялось выражение при выражении cos и sin в зависимости от tg?
До этого выражались cos и tg исходя из ранее описанных формул, сумма квадратов косинуса и синуса и частное синуса и косинуса.
А потом начали выражать cos и sin, но непонятно откуда взялось 1 / cos^2
Приложения:
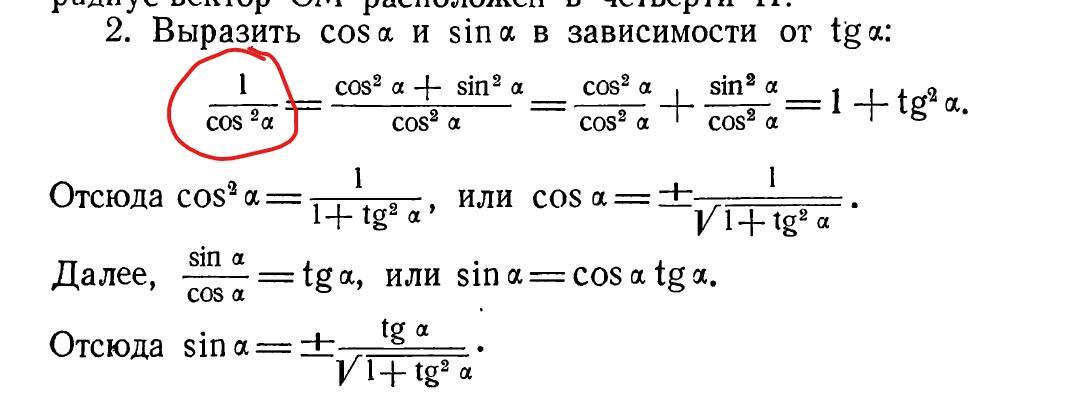
ВикаБач:
(sinA)^2 + (cosA)^2 =1. Это "теорема Пифагора". Раздели ЛЧ и ПЧ на (CosA)^2 и всё!!!
Ответы
Автор ответа:
1
Основное тригонометрическое тождество (по сути, теорема Пифагора, записанная в тригонометрических терминах):
Разделим обе части уравнения на
Похожие вопросы
Предмет: Русский язык,
автор: аташол3
Предмет: Английский язык,
автор: 759485
Предмет: Другие предметы,
автор: 1Софочка1
Предмет: Русский язык,
автор: valerapoddimov
Предмет: Математика,
автор: karina473281