Question

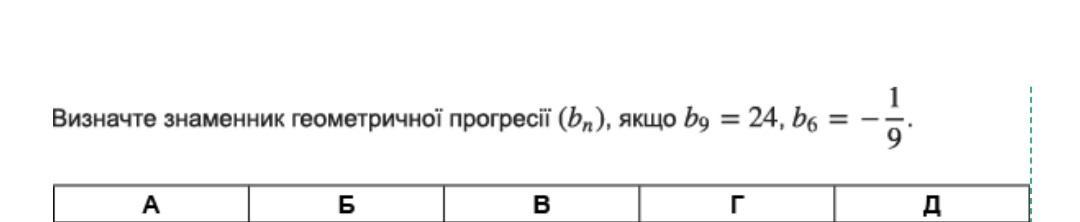
Помогите пожалуйста! Алгебра! Только нужно расписать чтобы было понятно

Answer 1

[1]   $b_{9} =24;$    $b_{6} =-\frac{1}{9};$   $q-?$

Формула n-ого члена геометрической прогрессии: $b_{n}={b_{1}q^{n-1}$

Распишем для $b_{6}$ и $b_{9} .$

$b_{6}={b_{1}q^{5}}\\b_{9}={b_{1}q^{8}}$

Составляем систему, чтобы выразить q (знаменатель геом.пр.) :

$\left \{ {{b_{6}={b_{1}q^{5} } \atop {b_{9}={b_{1}q^{8}}} \right.$

Решаем:

$\left \{ {{-\frac{1}{9} ={b_{1}q^{5} } \atop {24={b_{1}q^{8}}} \right.$      делим первое уравнение системы на второе, получаем:

$\frac{1}{q^3} =\frac{-\frac{1}{9} }{24} = > q=-6.$

[2]   $b_{2} +b_{4} =45$

$\\b_{2} * b_{4} =324$

$\\b_{1} -?$

Составим и решим систему, чтобы получить значения $b_{2}$ и $b_{4}$ :

$\left \{ {{b_{2} +b_{4} =45} \atop {b_{2} * b_{4} =324}} \right.$      $\left \{ {{b_{2}=45-b_{4} } \atop {b_{2} * b_{4} =324}} \right.$

$(45-b_{4} )b_{4} =324\\b_{4} ^2-45b_{4} +324=0$

Получаем корни:

$\\b_{4} =9$ или $\\b_{4} =36.$

Находим $b_{2}$ :

Так как $b_{2}=45-b_{4}$, то:

$b_{2}=45-9=36$ или $b_{2}=45-36=9.$

Заметим: что в $b_{4}$, что в $b_{2}$ - выходят одинаковые значения (36 и 9). От перестановки слагаемых сумма не меняется. Поскольку у нас возрастающая прогрессия, возьмем за $b_{4}=36$, а за $b_{2}=9.$

Чтобы найти первый член прогрессии, находим ещё $b_{3}$ и $q$ :

Формула: $b_{n}=\sqrt{b_{n+1}b_{n-1}}$

Решение: $b_{3}=\sqrt{36+9} =3*6=18.$

$q=\frac{b_{n+1}}{b_{n}} =\frac{b_{3}}{b_{2}} =2.$

И теперь мы можем с помощью формулы n-ого члена геометрической прогрессии: $b_{n}={b_{1}q^{n-1}$, вывести первый член прогрессии. Значит:

$b_{2}={b_{1}q}\\9={b_{1}*2}\\b_{1}=4,5.$