Предмет: Геометрия,
автор: theshadowmetya
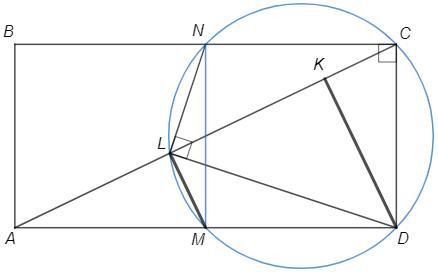
В прямоугольнике ABCD точка N — середина стороны BC. Точки K и L на диагонали AC таковы, что ∠DKC = ∠DLN = 90◦
. Докажите, что L — середина отрезка AK.
Ответы
Автор ответа:
1
∠DLN =∠C =90° => DLNC - вписанный
Пусть окружность пересекает AD в точке M.
DMLC - вписанный, ∠D=90° => ∠MLC=90° => ML||DK
DMNC - вписанный, ∠C=∠D=90° => ∠M=∠N=90°
DMNC - прямоугольник, MD=NC, M - середина AD
ML - средняя линия в △DAK => L - середина AK
Приложения:
cos20093:
Удивительно, у меня почти до буквы совпало, различие только в обозначении точки M (у меня F) :))) Еще можно (пишу в ваших обозначениях) AM*AD = AL*AC, откуда AL = (AD/2)*cos(CAD), это то же самое.
Похожие вопросы
Предмет: Английский язык,
автор: irviki26
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: 55555289
Предмет: Русский язык,
автор: dovgvika
Предмет: Математика,
автор: valeria200822