Предмет: Геометрия,
автор: theshadowmetya
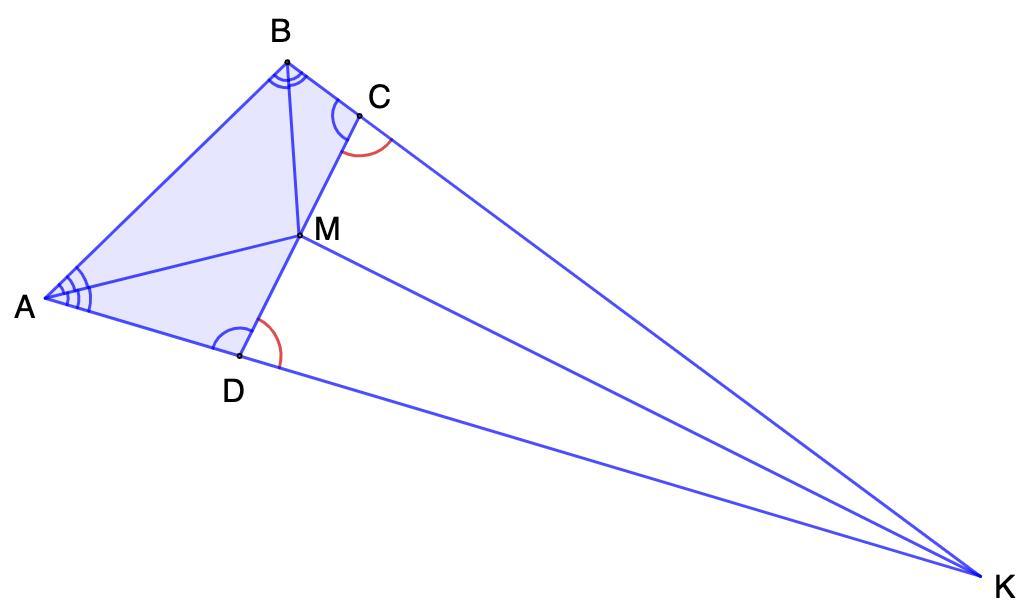
В выпуклом четырехугольнике ABCD известно, что ∠BCD = ∠CDA ⩾ 90◦
. Биссектрисы углов A и B пересекаются в точке M на стороне CD. Докажите, что M — середина CD.
cos20093:
Если продолжить стороны AD и BC до пересечения в точке E, то M - инцентр △ABE. При этом в △CDE точка M - основание биссектрисы EM, а сам △CDE равнобедренный из за заданного в условии равенства углов. ЧТД
Ответы
Автор ответа:
0
Ответ:
Доказали, что точка М - середина CD.
Объяснение:
В выпуклом четырехугольнике ABCD известно, что ∠BCD = ∠CDA ⩾ 90◦. Биссектрисы углов A и B пересекаются в точке M на стороне CD. Докажите, что M — середина CD.
Дано: АВСD - выпуклый четырехугольник;
∠BCD = ∠CDA ⩾ 90◦;
ВМ и АМ - биссектрисы ∠В и ∠А соответственно;
М ∈ CD;
Доказать: М - середина CD.
Доказательство:
Продолжим стороны ВС и АD до пересечения. Поставим точку К.
Соединим К и М.
1. Рассмотрим ΔАВК.
ВМ и АМ - биссектрисы ∠В и ∠А соответственно. (условие)
- Биссектрисы внутренних углов треугольника пересекаются в одной точке.
⇒ КМ - биссектриса ∠К.
2. Рассмотрим ΔDCK.
- Сумма смежных углов равна 180°.
⇒ ∠DCK = 180° - ∠BCD
∠CDK = 180° - ∠CDA
∠BCD = ∠CDA (условие)
⇒ ∠DCK = ∠CDK
- Если в треугольнике два равных угла, то этот треугольник равнобедренный.
⇒ ΔDCK - равнобедренный.
- В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой.
⇒ СМ = MD.
Доказали, что точка М - середина CD.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: irviki26
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: 55555289
Предмет: Русский язык,
автор: dovgvika
Предмет: Математика,
автор: valeria200822