Предмет: Математика,
автор: spxxx124
Поясніть як обчислити інтеграл.
Приложения:
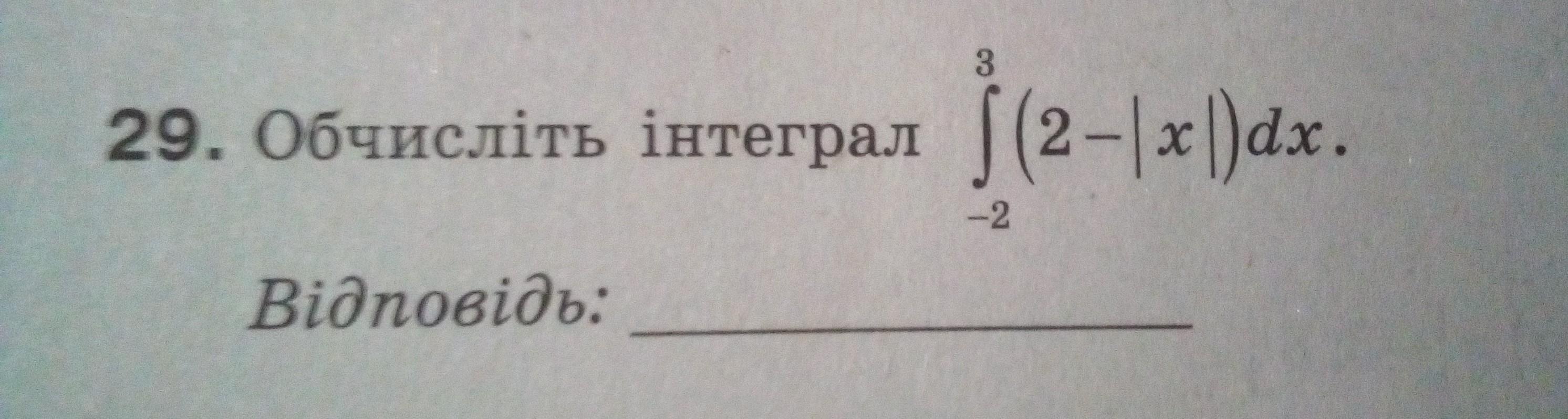
aarr04594:
Це завдання з ЗНО. Геометричній зміст інтеграла це площа фігури. Тому в даному випадку ви повинні побудувати графік функції у =2-|х|, а це просто . І визначити площу двох утворених трикутників в межах інтегрування. От і все. Ніякої первісної знаходити не треба.
Способ решения не указан, поэтому можно и через первообразную .
Можна. Але коли тільки 40 хв на 32 тестових питання, то це тільки порада. Я
Я думаю, що все корисне.
Вот вы знаете, что это из какого-то ЗНО , а я не знаю . И мне быстрее, чем чертить устно интеграл взять .
Ну так тому я і дала пораду автору питання.
Ответы
Автор ответа:
2
Ответ:
Правило раскрытия модуля:
Разобьём интервал интегрирования на два интервала , где x≥0 и
где х <0 . Это будут интервалы от -2 до 0 и от 0 до 3 .
По свойству определённого интеграла, его можно представить как сумму двух интегралов.
Применили формулу .
Автор ответа:
1
Вітаю. До Вашої уваги наступний спосіб розв'язання завдання
Відповідь: 3,5.
Приложения:

Так то графічним способом набагато швидше
І ще. Що важливо. Як би було завдання визначити площу , тоді площі треба додавати. Ну це так, для відома.
Зрозумів
Похожие вопросы
Предмет: Русский язык,
автор: охидея
Предмет: Русский язык,
автор: Алена11181988
Предмет: Русский язык,
автор: Alekc5194
Предмет: Физика,
автор: anatolievna2003
Предмет: Математика,
автор: Dingoy