Question

9 класс.
f(x) = 3x^2 + 8x + 5
Задание 1.Найти меньшее значение функции.
Задание 2.Указать промежуток роста графика функции
Задание 3.Найдите значение аргументов,при которых функция принимает не отрицательных значений

Answer 1

Ответ:

1.   $\displaystyle \boldsymbol {f_{min}=-\frac{1}{3} }$

2.   Функция возрастает на промежутке   $\displaystyle \boldsymbol {\bigg [-\frac{1}{3} ;\;+\infty\bigg)}$

3.   функция принимает не отрицательныe значения  при

$\displaystyle \boldsymbol { x \in \bigg(+\infty;\;-\frac{5}{3} \bigg]\; \cup\; \bigg[-1;\;+\infty\bigg)}$

Объяснение:

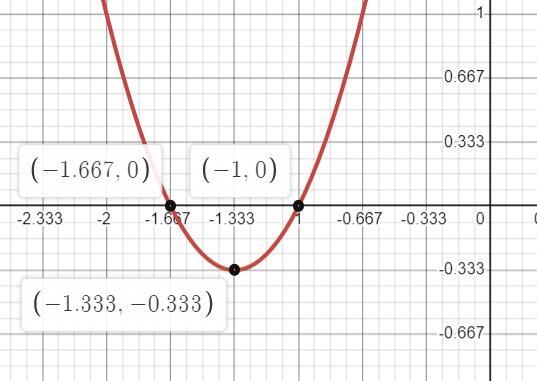
f(x) = 3x² +  8x + 5

1.   Найти меньшее значение функции.

График этой функции - парабола ветвями вверх.

Минимум функции достигается в вершине параболы.

Координата х₀ вершины по формуле

$\displaystyle x_0=-\frac{b}{2a} =-\frac{8}{6} =-\frac{4}{3}$

Тогда

$\displaystyle f_{min}=f(x_0) = 3*\bigg(-\frac{4}{3} \bigg)^2-8*\frac{4}{3} +5=\frac{16}{3} -\frac{32}{3} +\frac{15}{3} =\boxed {-\frac{1}{3} }$

2.  Указать промежуток роста графика функции

Функция возрастает на промежутке   $\displaystyle \bigg [-\frac{1}{3} ;\;+\infty\bigg)$

3. Найдите значение аргументов, при которых функция принимает не отрицательные значения

3x² +  8x + 5 ≥ 0

Сначала найдем нули функции

Приведем квадратное уравнение и применим  теорему Виета

$\displaystyle x^2+\frac{8}{3} x+\frac{5}{3} =0\\\\x_1+x_0=-\frac{8}{3} \\\\x_1*x_2=\frac{5}{3} \\\\\boxed {x_1=-1;\quad x_2=-\frac{5}{3} }$  - при этих значениях функция  f(x) = 0

И теперь, поскольку это парабола ветвями вверх,  неравенство  

3x² +  8x + 5 ≥ 0 выполняется при

$\displaystyle x \in \bigg(+\infty;\;-\frac{5}{3} \bigg]\; \cup\; \bigg[-1;\;+\infty\bigg)$