Question

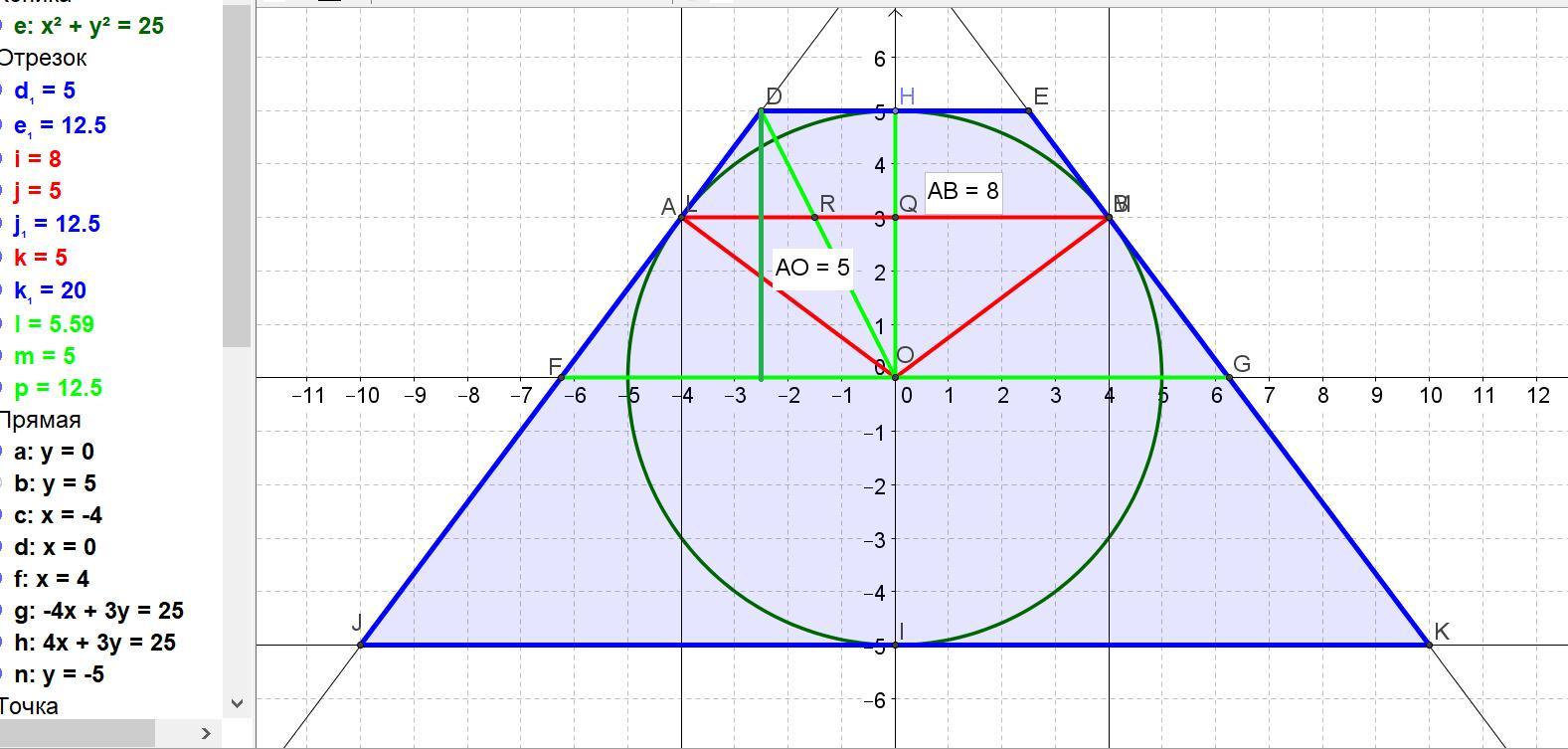
У рівнобедрену трапецію вписано коло радіусом 5 см. Знайти площу трапеції,
якщо відстань між точками дотику кола з бічними сторонами дорівнює 8 см.

Answer 1

Отрезок OD, как биссектриса, делит угол АОН пополам.

Длина АQ по заданию равна 8/2 = 4 см.

Тогда ОQ = √(5² - 4²) = √(25 – 16) = √9 = 3 см.

Используем формулу тангенса половинного угла ROQ:

tg(x/2)= √((1-cos⁡(x))/(1+cos⁡(x))).

Косинус угла AOQ = 3/5, подставим это значение в формулу.

tg(x/2)= √((1-3/5)/(1+3/5))=√(2/8)=1/2.

Определяем длину отрезка RQ = 3*(1/2) =(3/2) см.

По условию подобия треугольников находим длину половины верхнего основания трапеции.

DH/RQ = 5/3, отсюда DH = RQ*(5/3) = (3/2)*(5/3) = (5/2) см.

Получаем длину верхнего основания DE = 2*(5/2) = 5 см.

Если из точки D опустить перпендикуляр на среднюю линию трапеции, то аналогично из подобия треугольников находим её длину.

FG = 5 + 2((8/2) – (5/2))*(5/(5 – 3)) = 5 + 2*((3/2)*(5/2)) = 12,5 см.

Отсюда получаем ответ: S = 12,5*(2*5) = 125 см².