Question

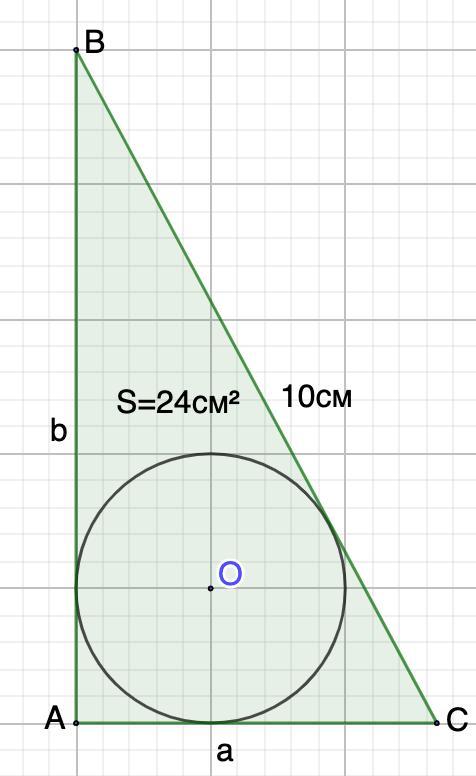
Гіпотенуза прямокутного трикутника дорівнює 10 см, а його площа 24 см². Знайти
радіус кола, вписаного у цей трикутник.

Answer 1

Ответ:

Радиус окружности, вписанной в этот треугольник равен 2 см.

Пошаговое объяснение:

Гипотенуза прямоугольного треугольника равна 10 см, а его площадь 24 см2. Найти радиус окружности, вписанной в этот треугольник.

Дано: ΔАВС - прямоугольный;

ВС = 10 см - гипотенуза;

S(ABC) = 24 см².

Окр.О,r - вписана в ΔАВС.

Найти: r - радиус вписанной окружности.

Решение:

• Радиус окружности, вписанной в прямоугольный треугольник найдем по формуле:

         $\displaystyle\bf \boxed {r=\frac{a+b-c}{2} }$,

где а и b - катеты, с - гипотенуза.

Гипотенуза нам известна с = ВС = 10 см.

Надо найти катеты.

Пусть катеты равны а см и b см.

Также нам известна площадь S(ABC) = 24 см²

• Площадь прямоугольного треугольника равна половине произведения катетов:

         $\displaystyle\bf \boxed {S=\frac{1}{2}ab }$

То есть:

$\displaystyle\bf \frac{1}{2}ab=24\;\;\;\Rightarrow \;\;\;ab=48$

• Теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы.

$\displaystyle\bf \Rightarrow a^2+b^2 = 100$

Получили систему уравнений:

$\displaystyle\bf \left \{ {{a^2+b^2=100} \atop {ab=48}} \right.$

Умножим второе уравнение на 2 и сложим уравнения:

$\displaystyle\bf \;\;\; \left \{ {{a^2+b^2=100} \atop {ab=48\;\;\;|\cdot2}} \right.\\\\ + \left \{ {{a^2+b^2=100} \atop {2ab=96$

    a² + 2ab + b² = 196

    (a + b)² = 196

⇒ (a + b) = 14

* отрицательные значения не берем, так как они не соответствуют условию задачи.

Зная сумму катетов, можем найти радиус:

$\displaystyle\bf r=\frac{14-10}{2} =2\;_{(CM)}$

Радиус окружности, вписанной в этот треугольник равен 2 см.