Question

СРОЧНО!!!
Із точки що лежить поза площиною проведено дві похилі між кутом 30градусів і дорівнюють 2корінь 3см.Іх проекціі утворюють між собою кут 120 градусів.Знайдіть відстань між основами похилих

Answer 1

Ответ:

Расстояние между основаниями наклонных равно 3√3.

Объяснение:

Из точки лежащей вне плоскости проведены две наклонные под углом 30° и равны 2√3 см. Их проекции образуют между собой угол 120°. Найдите расстояние между основаниями наклонных.

-------

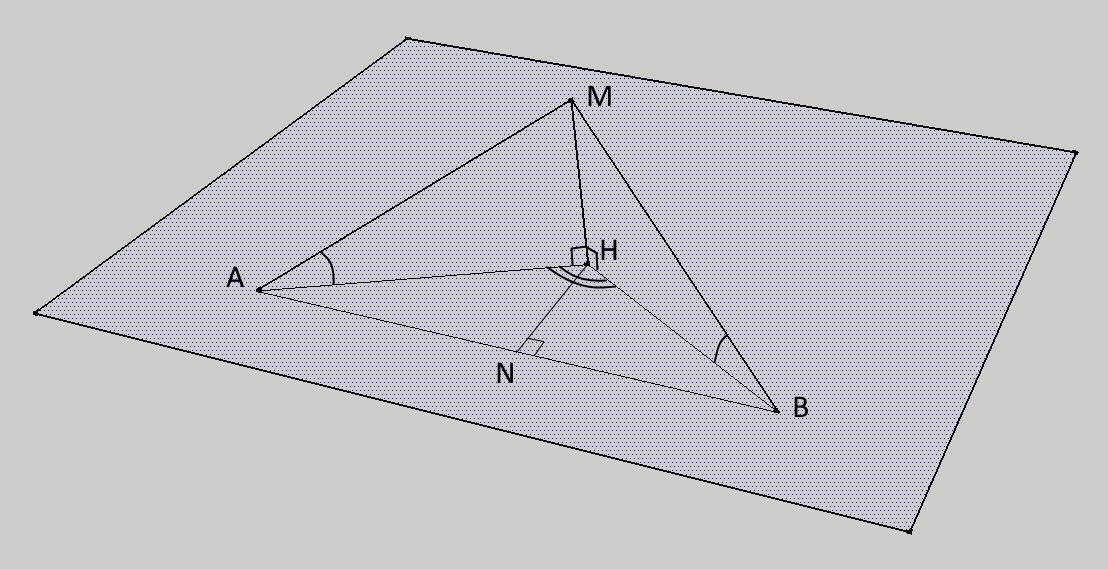
Дано:

MA = MB = 2√3

MH ⊥ к заданной плоскости

∠MAН = ∠MBН = 30°

∠AHB = 120°

AB = ?

-------

Треугольники MAН и MBН прямоугольные, ∠MAН = ∠MBН, а значит подобные углы треугольников равны, MA = MB, MH - общая:

ΔMAН = ΔMBН

AH = BH = MA×cos(30°) = 2√3×(√3/2) = 3 см

Треугольник AHB - равнобедренный, проведем из точки H высоту HN, она же будет биссектрисой:

∠AHN = ∠BHN = 60°

Треугольники AHN и BHN прямоугольные и равные:

AN = BN = AH×sin(60°) = 3×(√3/2)

AB = AN+BN = AN×2 = 3×(√3/2)×2 = 3√3

#SPJ1