Предмет: Алгебра,
автор: marinokivanova
Помогите пожалуйста!!!!
Знайдіть суму натуральних чисел, що входять до області визначення функції
Найдите сумму натуральных чисел, входящих в область определения функции
Приложения:
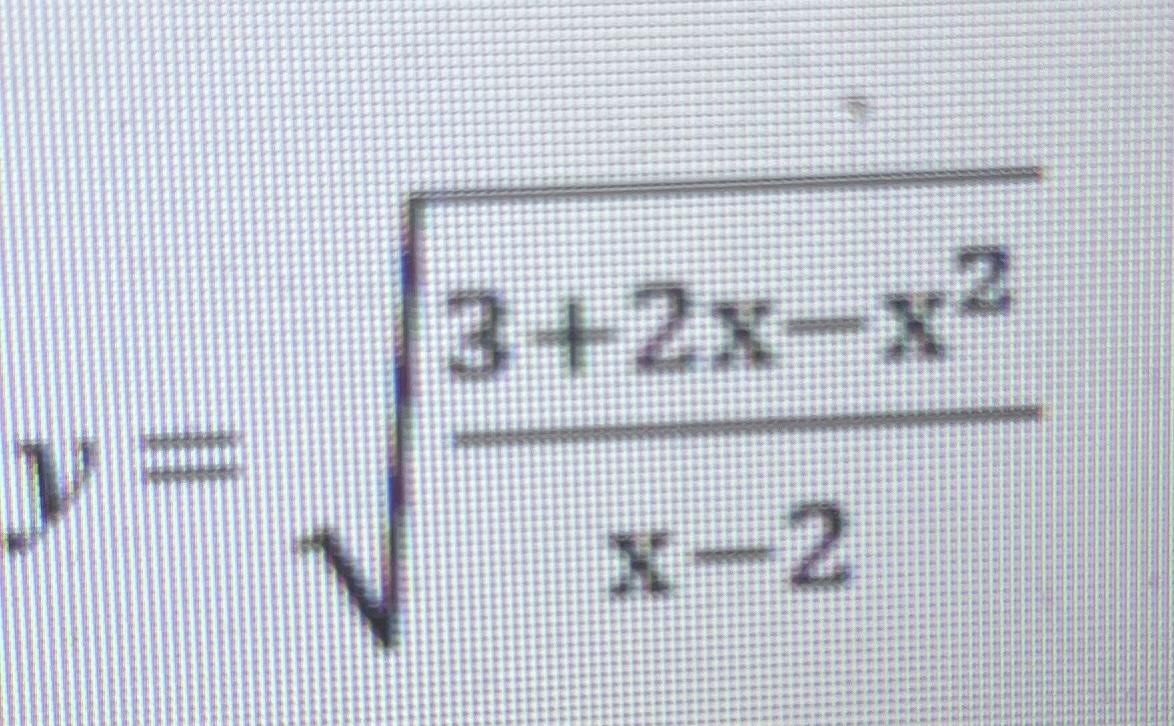
Ответы
Автор ответа:
1
Ответ:
3
Объяснение:
подкоренное выражение неотрицательно, решаем методом интервалов,из натуральных только (2;3]. Подходит только 3
Приложения:
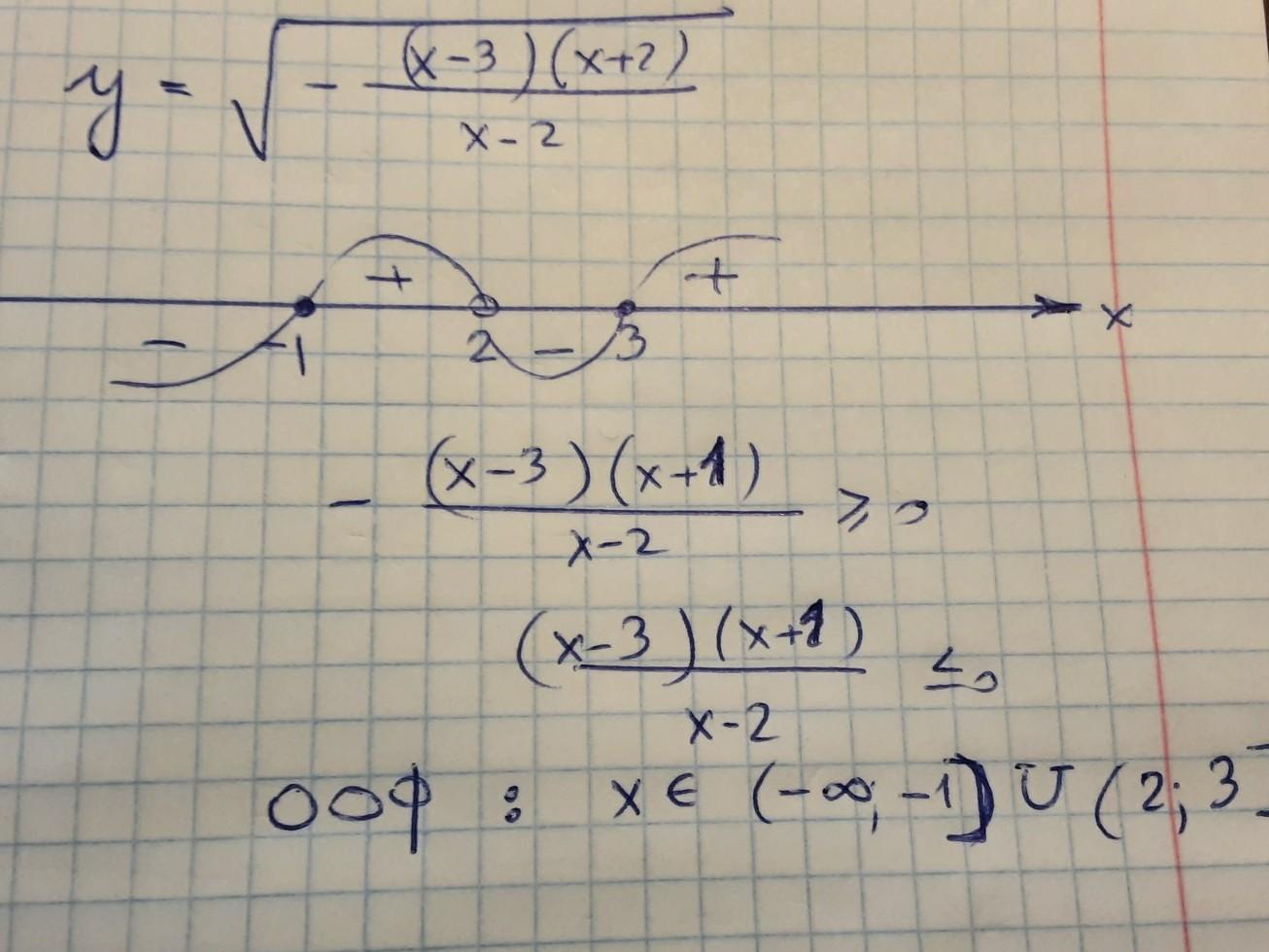
Автор ответа:
4
Подкоренное выражение корня чётной степени должно быть неотрицательным , то есть ≥ 0 .
В область определения этой функции входит только одно натуральное число 3 .
Похожие вопросы
Предмет: Другие предметы,
автор: APPONastasilu
Предмет: Русский язык,
автор: Алта777
Предмет: Окружающий мир,
автор: DestinyHope
Предмет: Английский язык,
автор: yana8730