Предмет: Математика,
автор: sas98312
будь-ласка, допоможіть і поясніть
Приложения:
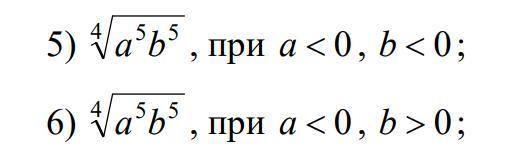
Ответы
Автор ответа:
1
Ответ:
Формула извлечения корня чётной степени: .
Обращаем внимание на то, что под корнем 4 степени записано произведение отрицательных чисел, значит само произведение положительно и имеет право находиться под корнем чётной степени .
Под корнем чётной степени записано произведение , которое при отрицательном а и положительном b будет отрицательным. А под корнем чётной степени отрицательные выражения не могут стоять. то есть выражение
не имеет смысла при
, корень извлечь нельзя .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: YuriyYarema
Предмет: Русский язык,
автор: Амирбог
Предмет: Русский язык,
автор: 123жас
Предмет: Математика,
автор: svetik2808
Предмет: Қазақ тiлi,
автор: Аноним