Question

Заполните пропуски в тексте, чтобы получилось правильное решение.


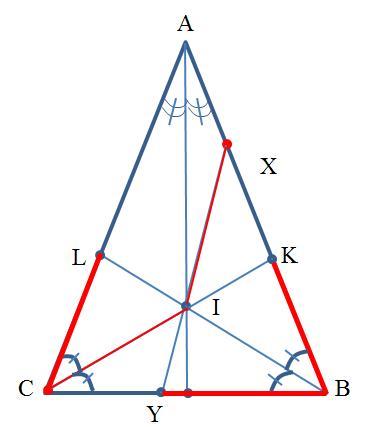
Задача. В равнобедренном треугольнике ABC (AB=AC) биссектриса BL пересекается с биссектрисой угла A в точке I. Точка X на стороне AB выбрана так, что BX=BC. Прямая XI пересекает основание BC в точке Y. Докажите, что LC=BY.




Решение. Заметим, что точки X и


C


L


Y

симметричны относительно прямой


AI


BI


CI

, поэтому длина отрезка BY равна длине отрезка


BK


IK


XK

, где K — точка пересечения биссектрисы CI со стороной AB. Осталось заметить, что отрезок


BK


CK


XK

равен отрезку CL, поскольку они симметричны относительно прямой


AI


BI


CI

.

Answer 1

Ответ и Объяснение:

Задача. В равнобедренном треугольнике ABC (AB=AC) биссектриса BL пересекается с биссектрисой угла A в точке I. Точка X на стороне AB выбрана так, что BX=BC. Прямая XI пересекает основание BC в точке Y. Докажите, что LC=BY.

Доказательство. Рисунок в приложении.

Заметим, что точки X и C симметричны относительно прямой BL (потому что BL – биссектриса угла CBX, а BX = BC), поэтому прямые XI и CI симметричны относительно этой же прямой, откуда длина отрезка BY равна длине отрезка BK, где K - точка пересечения биссектрисы CI со стороной AB.

Осталось заметить, что отрезок BK равен отрезку LC, поскольку они симметричны относительно прямой AI.

#SPJ5