Question

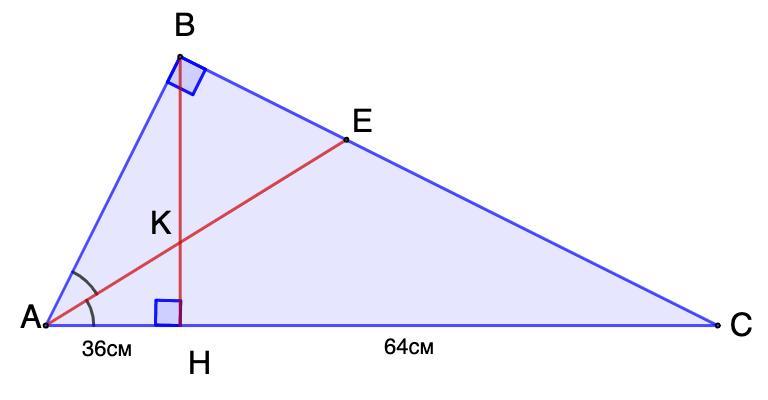
1.)3 вершини прямого кута прямокутника проведено перпендикуляр, який ділить гіпотенузу на вiдрiзки 36 і 64 см. Обчислить вiдрiзки, на які ділять бісектриса більшого гострого кута цей перпендикуляр.
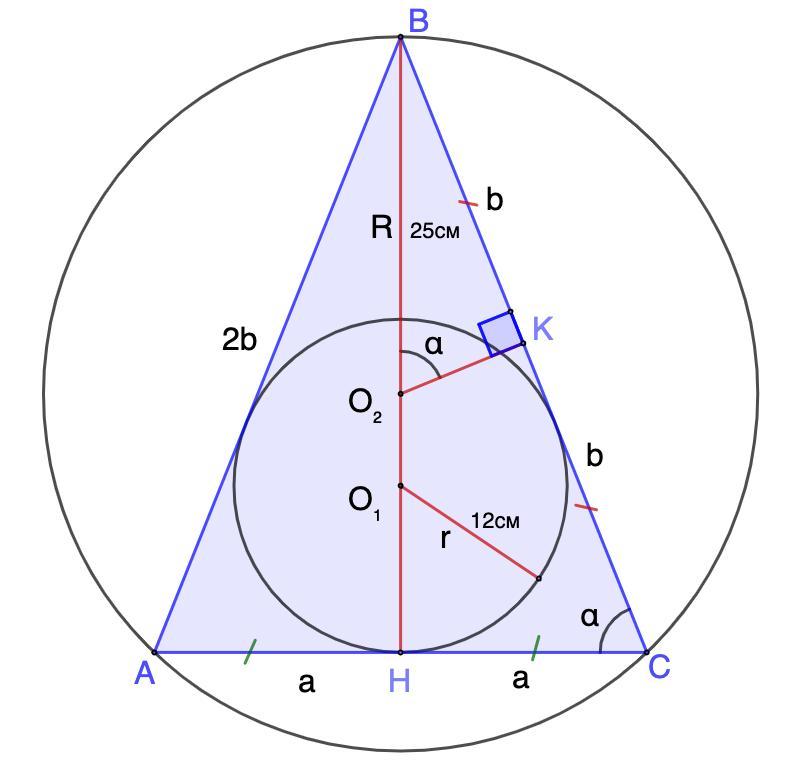
2.)У рівнобедреному трикутнику радіуси вписаного і описаного кiл вiдповiдно дорівнюють 12 і 25 см. Обчислити периметр трикутника.

Answer 1

Ответ:

1.) Отрезки, на которые делит биссектриса большего острого угла этот перпендикуляр, равны 30 см и 18 см, начиная от вершины.

2.) Периметр треугольника равен 128 см или 28√21 см.

Объяснение:

1.) Из вершины прямого угла прямоугольного треугольника проведен перпендикуляр, который делит гипотенузу на отрезки 36 см и 64 см. Вычислить отрезки, на которые делит биссектриса большего острого угла этот перпендикуляр.

Дано: ΔАВС - прямоугольный;

ВН ⊥ АС;

АН = 36 см; НВ = 64 см.

АЕ - биссектриса.

АЕ ∩ ВН = К.
Найти: ВК и КН.

Решение:

1. ВН ⊥ АС (условие) ⇒ ВН - высота ΔАВС.

Используем метрические соотношения в прямоугольном треугольнике:

• Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу, а квадрат каждого катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

Найдем АВ и ВН.

АВ² = АН · АС = 36 · (36 + 64) = 36 · 100

АВ = 6 · 10 = 60 (см)

ВН² = ВН · НС = 36 · 64

ВН = 6 · 8 = 48 (см)

2. Рассмотрим ΔАВН - прямоугольный.

АК - биссектриса (условие)

• Биссектриса  угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.

⇒

$\displaystyle\bf \frac{AB}{AH} =\frac{KB}{KH}$

$\displaystyle\bf \frac{KB}{KH}=\frac{60}{36} =\frac{5}{3}$

Пусть КВ = 5х см, тогда КН = 3х см.

ВН = 48 см.

Составим уравнение:

5х + 3х = 48

8х = 48

х = 6

⇒ КВ = 30 см; КН = 18 см.

2.) В равнобедренном треугольнике радиусы вписанного и описанного окружностей соответственно равны 12 см и 25 см. Вычислить периметр треугольника.

Дано: ΔАВС - равнобедренный.

Окр.О₁,r - вписана в ΔАВС;

Окр.О₂,R - описана около ΔАВС;

r = 12 см, R = 25 см.

Найти: Р(АВС).

Решение:

Проведем ВН - высоту.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ ВН - серединный перпендикуляр АС.

• Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров.

Проведем О₂К - серединный перпендикуляр ВС.

⇒ О₂ - центр окружности, описанной около ΔАВС.

Пусть ВК = КС = b, AH = HC = a

⇒ AB = BC = 2b, AC = 2a.

Пусть ∠ВО₂К = ∠С = α

Формулы радиусов вписанной и описанной окружностей:

$\displaystyle\bf \boxed {R=\frac{abc}{4S} },\;\;\;\;\;\boxed {r=\frac{2S}{P} }$,

где a, b, c - стороны треугольника, S - площадь треугольника, Р - его периметр.

Из формул выразим S.

1.

$\displaystyle\bf S=\frac{abc}{4R} \\\\S=\frac{2b\cdot{2b}\cdot{2a}}{4\cdot25} =\frac{2ab^2}{25}\;\;\;\;\;(1)$

2.

$\displaystyle\bf S=\frac{rP}{2}\\ \\S=\frac{12\cdot(2b+2b+2a)}{2} =6(4b+2a)\;\;\;\;\;(2)$

Приравняем (1) и (2)

$\displaystyle\bf \frac{2ab^2}{25}=6(4b+2a)\;\;\;|\cdot 25\\\\2ab^2=25\cdot6(4b+2a)\\\\ab^2=75(4b+2a)\;\;\;\;\;(3)$

3. Рассмотрим ΔHBC - прямоугольный.

$\displaystyle\bf \frac{HC}{BC}=cos\;\alpha$     или     $\displaystyle\bf \frac{a}{2b}=cos\;\alpha$

⇒ a = 2b · cosα

Подставим значение а в равенство (3):

(2b cosα) · b² = 75 (4b + 4b cosα)

2b³cosα = 75 · 4b · (1 + cosα)   |:(2b)

b²cosα = 150(1 + cosα)     (4)

4. Рассмотрим ΔО₂ВК - прямоугольный.

$\displaystyle\bf \frac{O_2K}{O_2B}=cos\;\alpha \;\;\;$     или     $\displaystyle\bf \frac{O_2K}{25} =cos\;\alpha$

O₂K = 25cosα

По теореме Пифагора:

КВ² = О₂В² - О₂К²

b²= 625 - 625cos²α = 625(1 - cos²α)=625(1 - cosα)(1 + cosα)

Подставим b² в равенство (4):

625(1 - cosα)(1 + cosα) · cosα = 150(1 + cosα)     |:25(1 + cosα)

25(1 - cosα) · cosα = 6

25 cosα - 25 cos²α - 6 = 0

cos α = x

25x² - 25x + 6 = 0

D = 625 - 600 = 25

√D = 5

$\displaystyle\bf x_1=\frac{25+5}{50}=\frac{3}{5}\;\;\;\;\;x_2=\frac{25-5}{50}=\frac{2}{5}$

Получили два значения:

$\displaystyle\bf cos\alpha =\frac{3}{5},\;\;\;\;\;cos\alpha=\frac{2}{5}$

Найдем стороны:

1) cosα = 3/5

$\displaystyle\bf b^2=625-625\cdot\frac{9}{25}=400\\ \\ b=20$

$\displaystyle\bf a=2\cdot20\cdot{\frac{3}{5} }=24$

⇒ АВ = ВС = 40 см; АС = 48 см

Такой треугольник существует.

Р = 40 + 40 + 48 = 128 (см)

2) cosα = 2/5.

$\displaystyle\bf b^2=625-625\cdot\frac{4}{25}=525\\ \\ b=5\sqrt{21}$

$\displaystyle\bf a=2\cdot5\sqrt{21} \cdot{\frac{2}{5} }=4\sqrt{21}$

⇒ АВ = ВС = 10√21 см; АС = 8√21 см

Такой треугольник тоже существует.

Р = 10√21 + 10√21 + 8√21 = 28√21 (см)

Периметр треугольника равен 128 см или 28√21 см.

Если Вы знаете формулу Эйлера, то можно решить проще (см. вложение.

• В треугольнике радиус R описанной окружности и радиус r вписанной окружности связаны с расстоянием d между их центрами соотношением: d² = R² - 2Rr.

#SPJ1