Предмет: Математика,
автор: 120ka1
Знайдіть найбільше і найменше значення функції на відрізку [а, б]
Приложения:
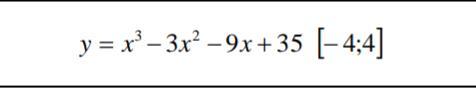
Ответы
Автор ответа:
3
Найти наибольшее и наименьшее значение функции y=x^3-3x^2-9x+35 на промежутке [-4;4].
Ответ:
Наибольшее значение функции на промежутке [-4;4] - y(-1)=40; наименьшее - у=(-4)=(-41).
Пошаговое объяснение:
Для начала вспомним теорию. Алгоритм нахождения наибольшего и наименьшего значений функции на заданном промежутке:
- Найти производную ф-ции.
- Находим критические точки, которые принадлежат заданному промежутку.
- Вычисляем значения функции в критических точках, которые принадлежат заданному промежутку и в крайних точках промежутка.
- Выбираем наибольшее и наименьшее из них.
1. Найдём производную функции.
2. Находим критические точки, которые принадлежат заданному промежутку.
3. Вычисляем значения функции в критических точках, которые принадлежат заданному промежутку и в крайних точках промежутка.
4. Выбираем наибольшее и наименьшее из получившихся значений:
Похожие вопросы
Предмет: Английский язык,
автор: ambiguous
Предмет: Қазақ тiлi,
автор: Nikotyan
Предмет: Английский язык,
автор: ambiguous
Предмет: Математика,
автор: Superman289
Предмет: География,
автор: ekulikovskij4